Program in R to Read Images and Output a Number

ane Quick kickoff
two Loading and saving images
three Loading and saving videos
4 Displaying images and videos
5 How images are represented
half-dozen Coordinates
7 The cimg class
eight Prototype lists
9 Pixel sets (pixsets)
10 Splitting and concatenating images
11 Split, utilise, combine
12 Sub-images, pixel neighbourhoods, etc.
13 Denoising
14 Colour spaces
fifteen Resizing, rotation, etc.
16 Warping
17 Lagged operators
eighteen Filtering
19 FFTs and the periodic/smoothen decomposition
twenty Morphology

Simon Barthelmé (GIPSA-lab, CNRS)

This documentation covers imager version 0.40. Some functions may be unavailable in older versions. Follow imager development on github.

Beginners: have a look at the tutorial first.

Quick start

Here'due south an example of imager in activeness:

            library(imager)   file <- system.file('extdata/parrots.png',parcel='imager') #system.file gives the full path for a file that ships with a R package #if you already have the total path to the file you want to load but run: #im <- load.epitome("/somedirectory/myfile.png") im <- load.prototype(file)  plot(im) #Parrots!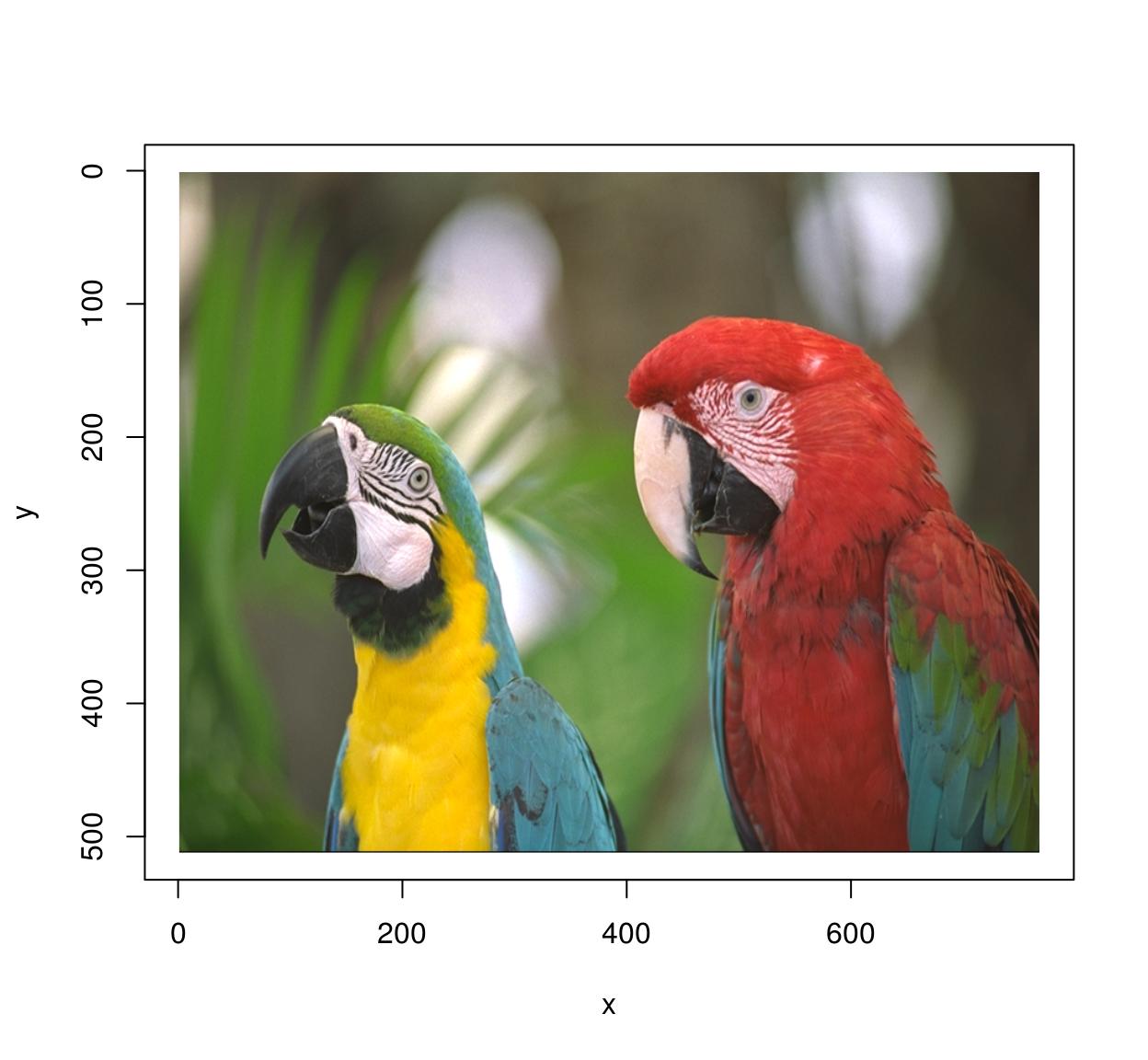

            im.blurry <- isoblur(im,10) #Blurry parrots! plot(im.blurry)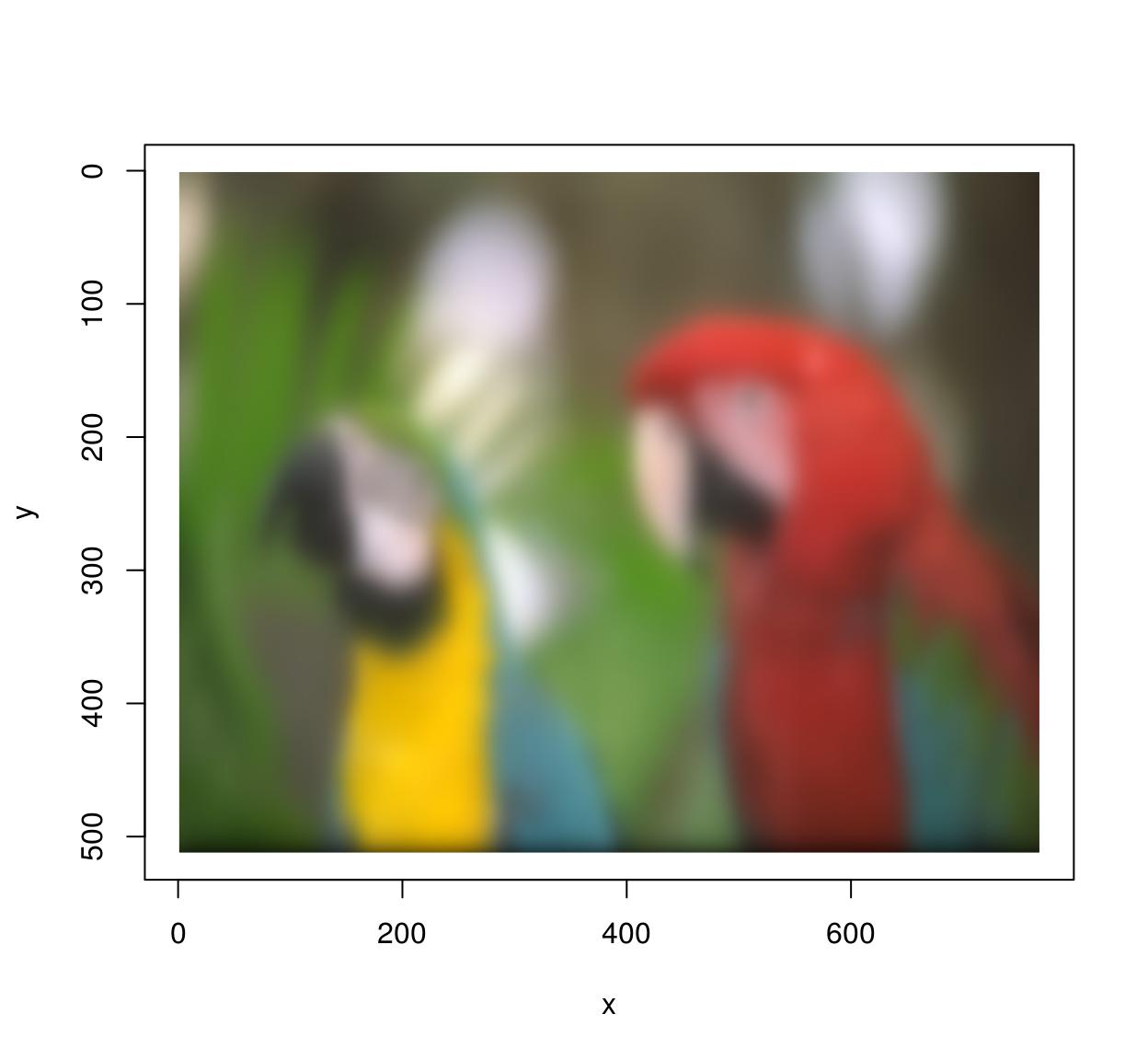

            im.xedges <- deriche(im,2,lodge=2,axis="x") #Edge detector along x-axis plot(im.xedges)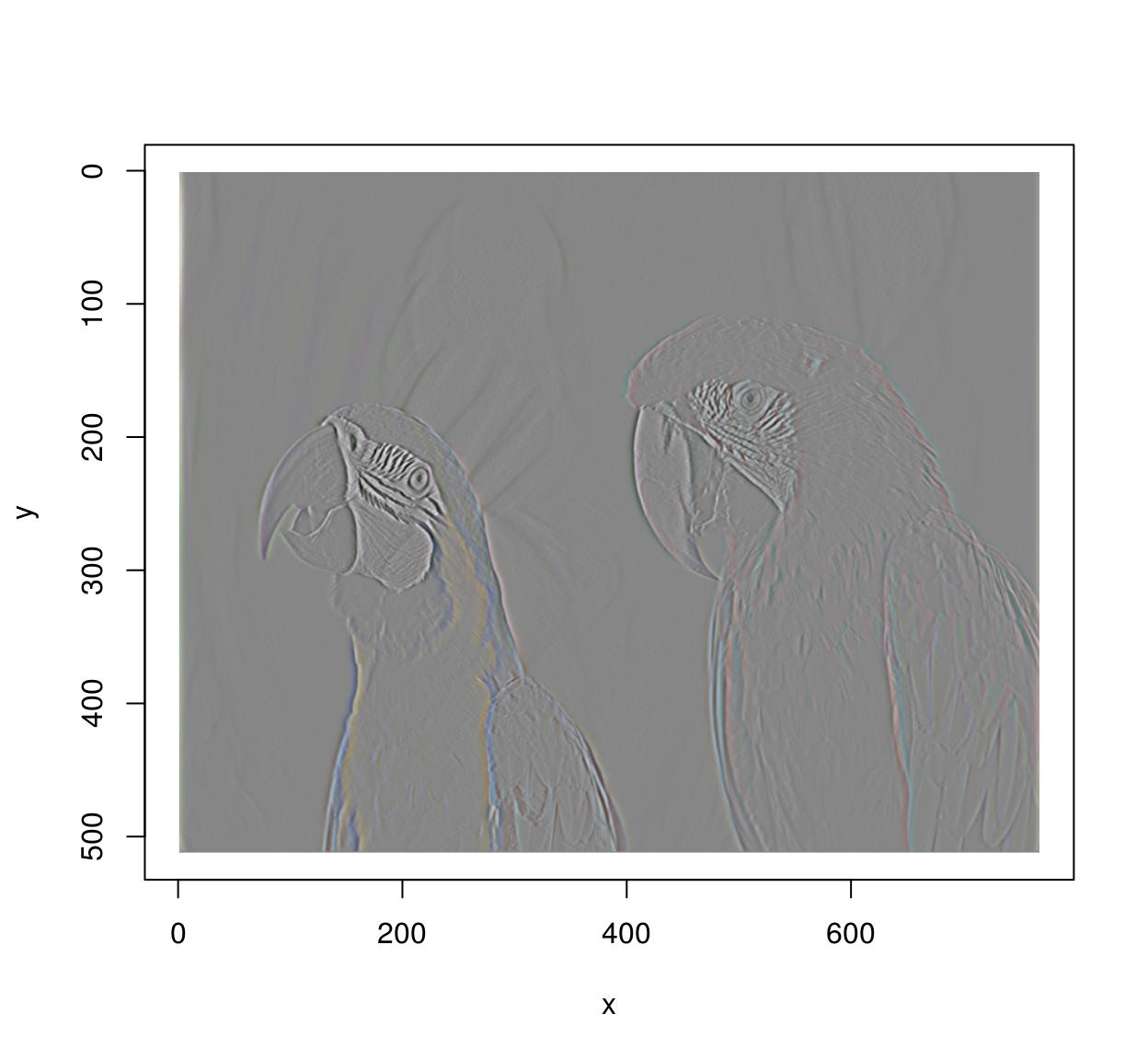

            im.yedges <- deriche(im,ii,order=2,axis="y") #Edge detector along y-axis plot(im.yedges)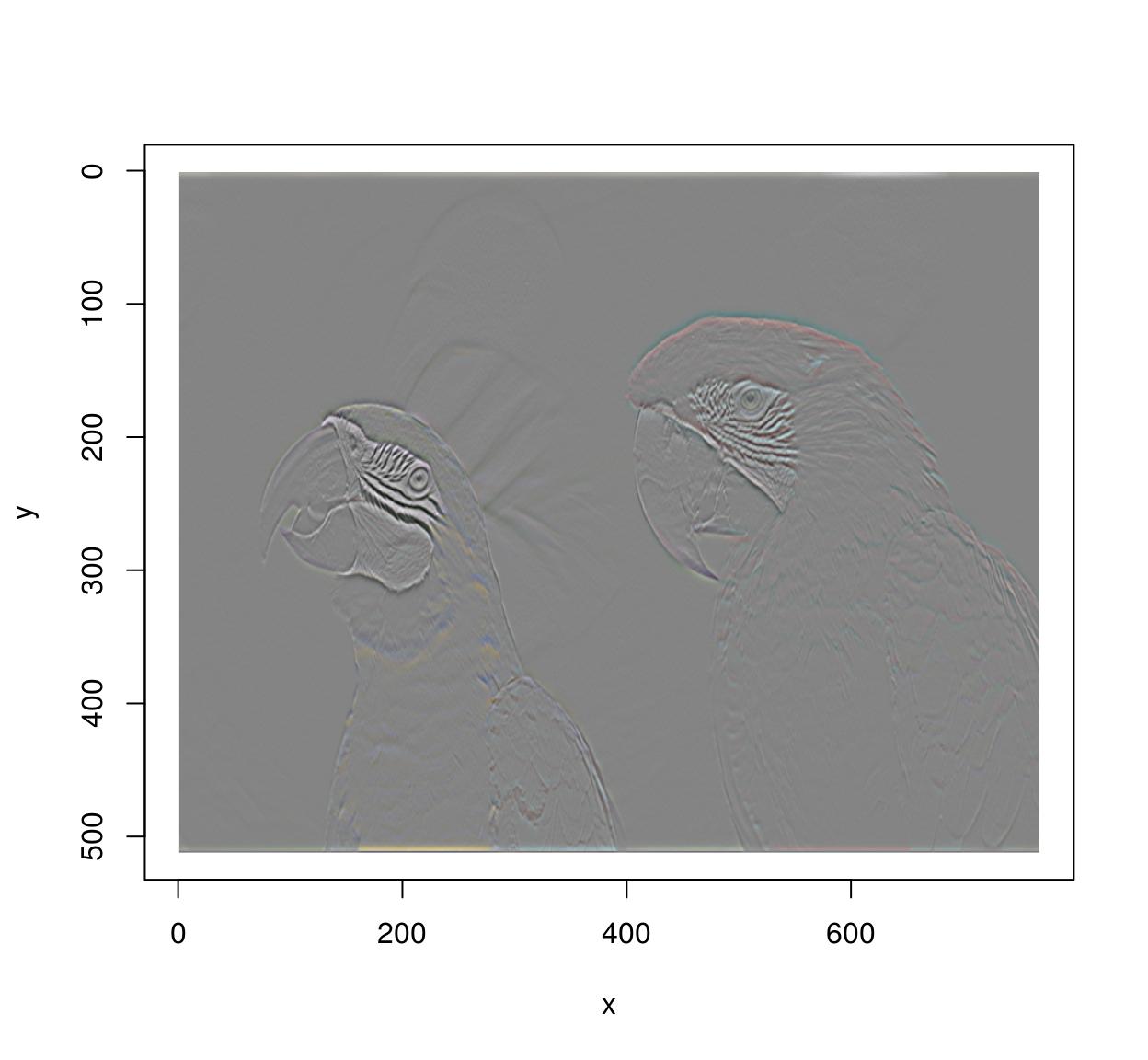

            #Chain operations using the pipage operator (from magrittr) deriche(im,2,order=2,axis="x") %>% deriche(2,order=2,axis="y") %>% plot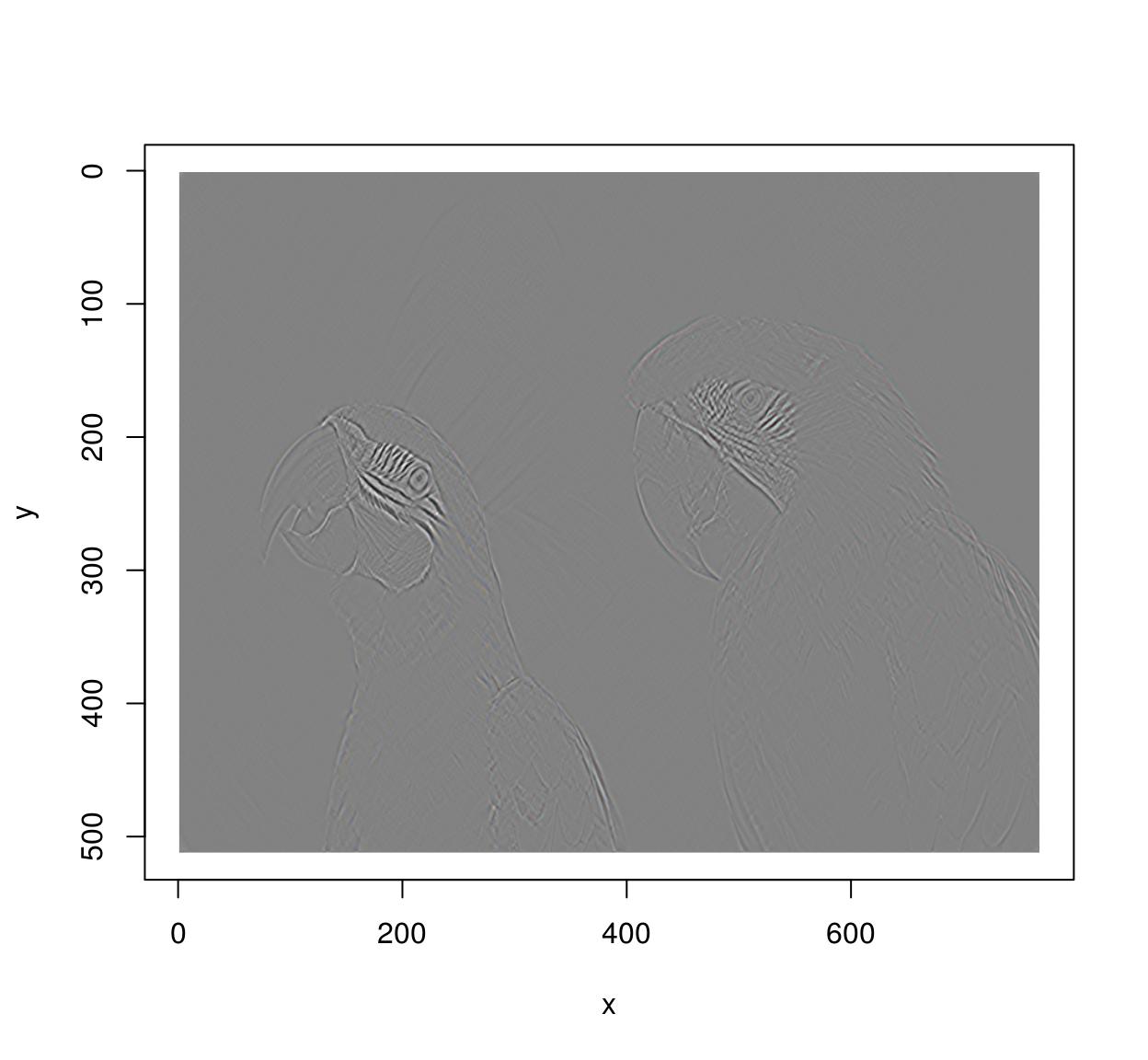

            #Another example of chaining: epitome gradient along x and y axes layout(matrix(1:2,1,2)); grayscale(im) %>% imgradient("xy") %>% plot(layout="row")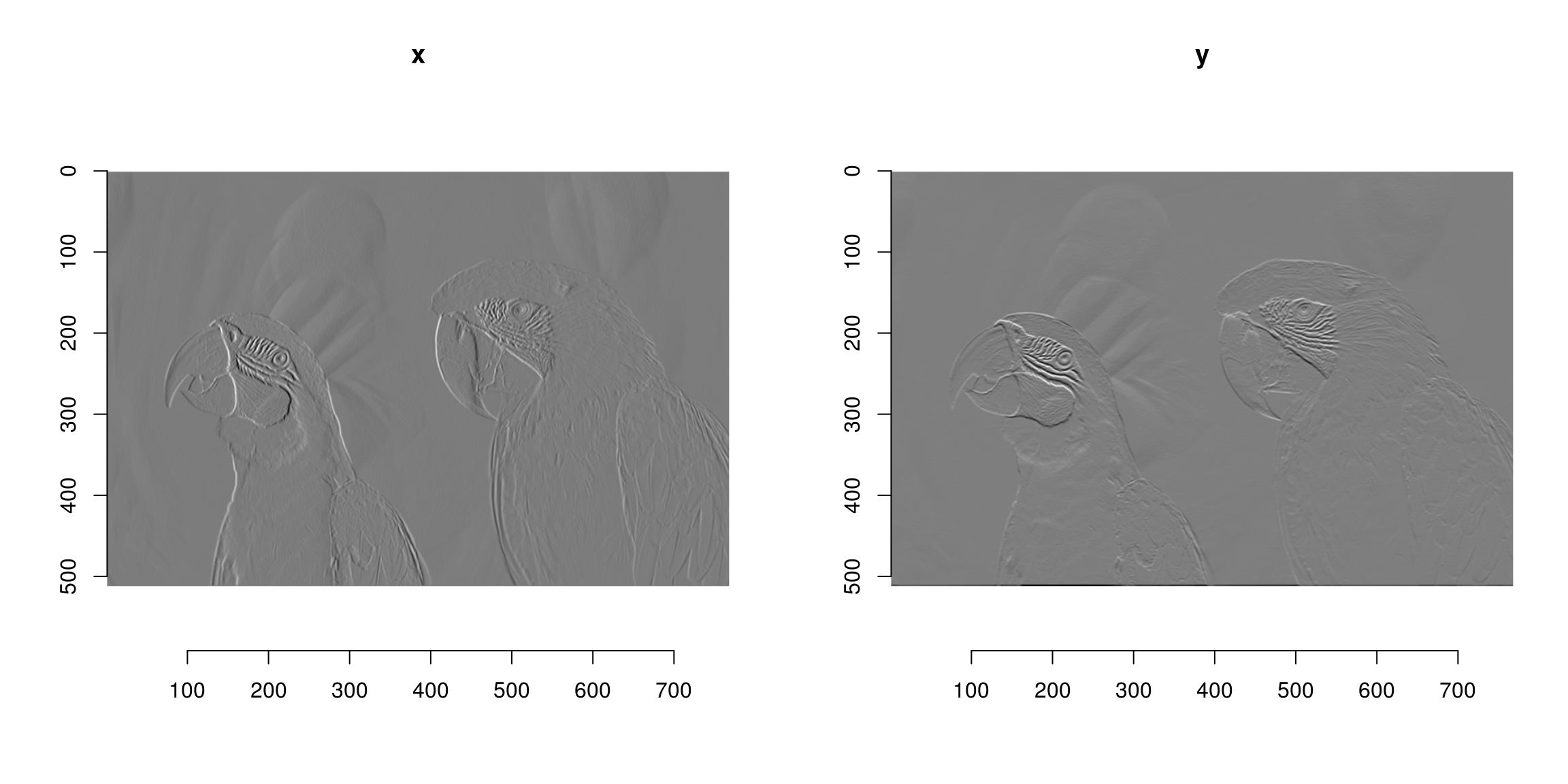

            #If ffmpeg is present, nosotros tin load videos besides: tennis <- load.video(system.file('extdata/tennis_sif.mpeg',parcel='imager'))  plot(tennis,frame=i)

            plot(tennis,frame=5)

In the next example, we convert the video to grayscale, run a motility detector, and combine both videos to display them side-past-side:

            lawn tennis.g <- grayscale(lawn tennis) motion <- deriche(tennis.g,ane,order=1,axis="z")^2 #Differentiate along z centrality and square combined <- list(motility/max(motion),tennis.g/max(tennis.grand)) %>% imappend("x") #Paste the ii videos together

In an interactive session y'all can run play(combined) to view the results.

Loading and saving images

Apply load.prototype and save.image. imager supports PNG, JPEG and BMP natively. If you need to admission images in other formats you'll demand to install ImageMagick.

            file <- organization.file('extdata/parrots.png',package='imager') parrots <- load.epitome(file) #The file format is defined past the extension. Hither we save equally JPEG imager::salvage.paradigm(parrots,"/tmp/parrots.jpeg") #We phone call imager::relieve.paradigm to avoid ambiguity, as base R already has a relieve.image function

You tin can load files from your hard drive or from a URL. Loading from URLs is useful when scraping web pages, for example. The following piece of code searches for pictures of parrots (using the rvest package), then loads the starting time four pictures it finds:

            library(rvest) #Run a search query (returning html content) search <- read_html("https://www.google.com/search?site=&tbm=isch&q=parrot")  #Catch all <img> tags, go their "src" attribute, a URL to an epitome urls <- search %>% html_nodes("img") %>% html_attr("src") #Become urls of parrot pictures  #Load the first iv, return as image list, display map_il(urls[1:4],load.image) %>% plot

Loading and saving videos

If yous need to load and salvage videos delight install ffmpeg for videos.

To load videos, use load.video:

            fname <- organisation.file('extdata/tennis_sif.mpeg',package='imager') tennis <- load.video(fname)

Use skip.to to set the initial frame, and frames to set the number of frames to take hold of:

            #Skip to time = 2s, and grab the next 3 frames vid <- load.video(fname,skip.to=two,frames=4) #Display individual frames (see imsplit below) imsplit(vid,"z") %>% plot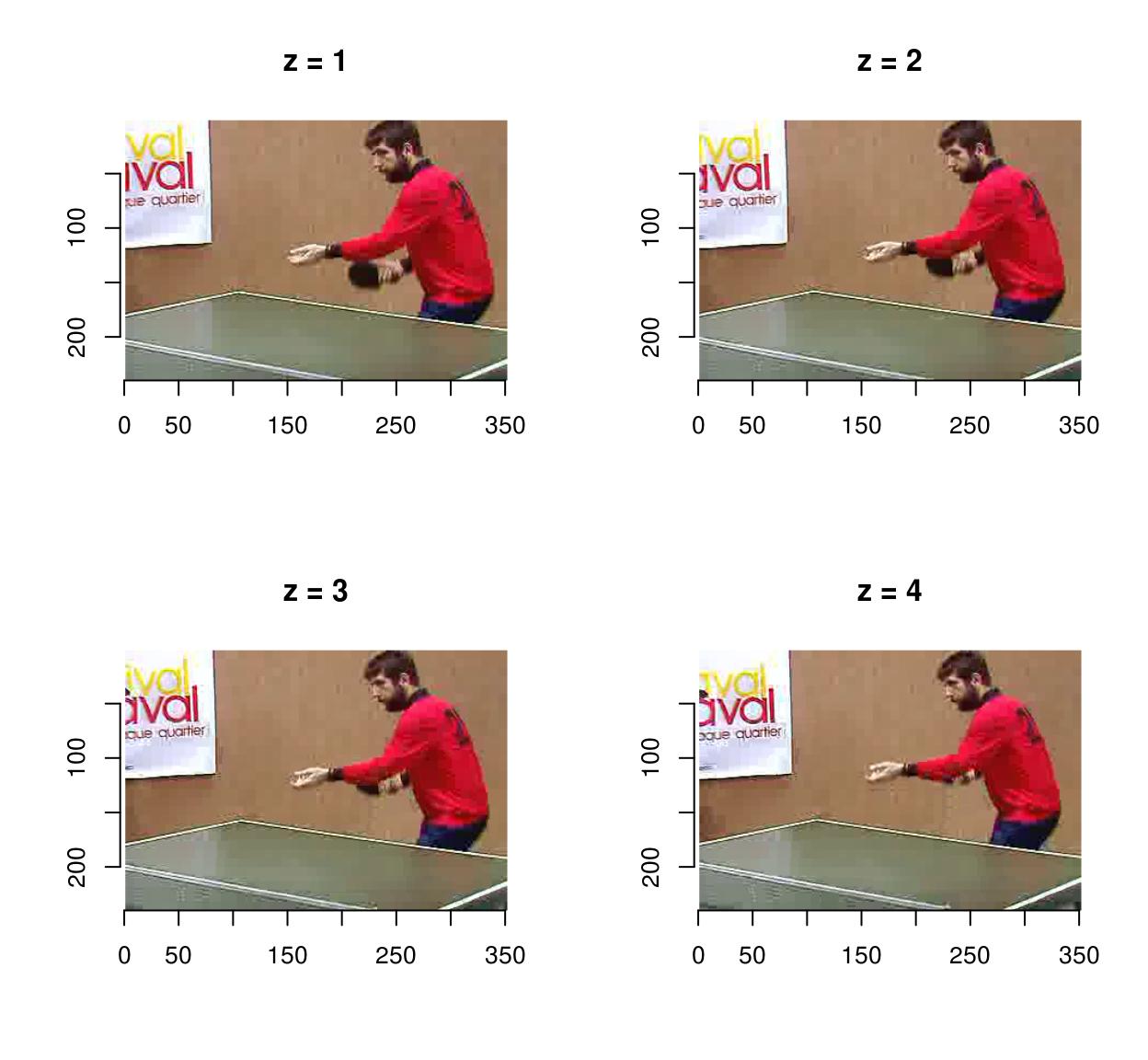

Apply fps to set the frame acquisition rate:

            vid <- load.video(fname,fps=1) #i frame per sec #The outcome is half-dozen frames, one per sec imsplit(vid,"z") %>% plot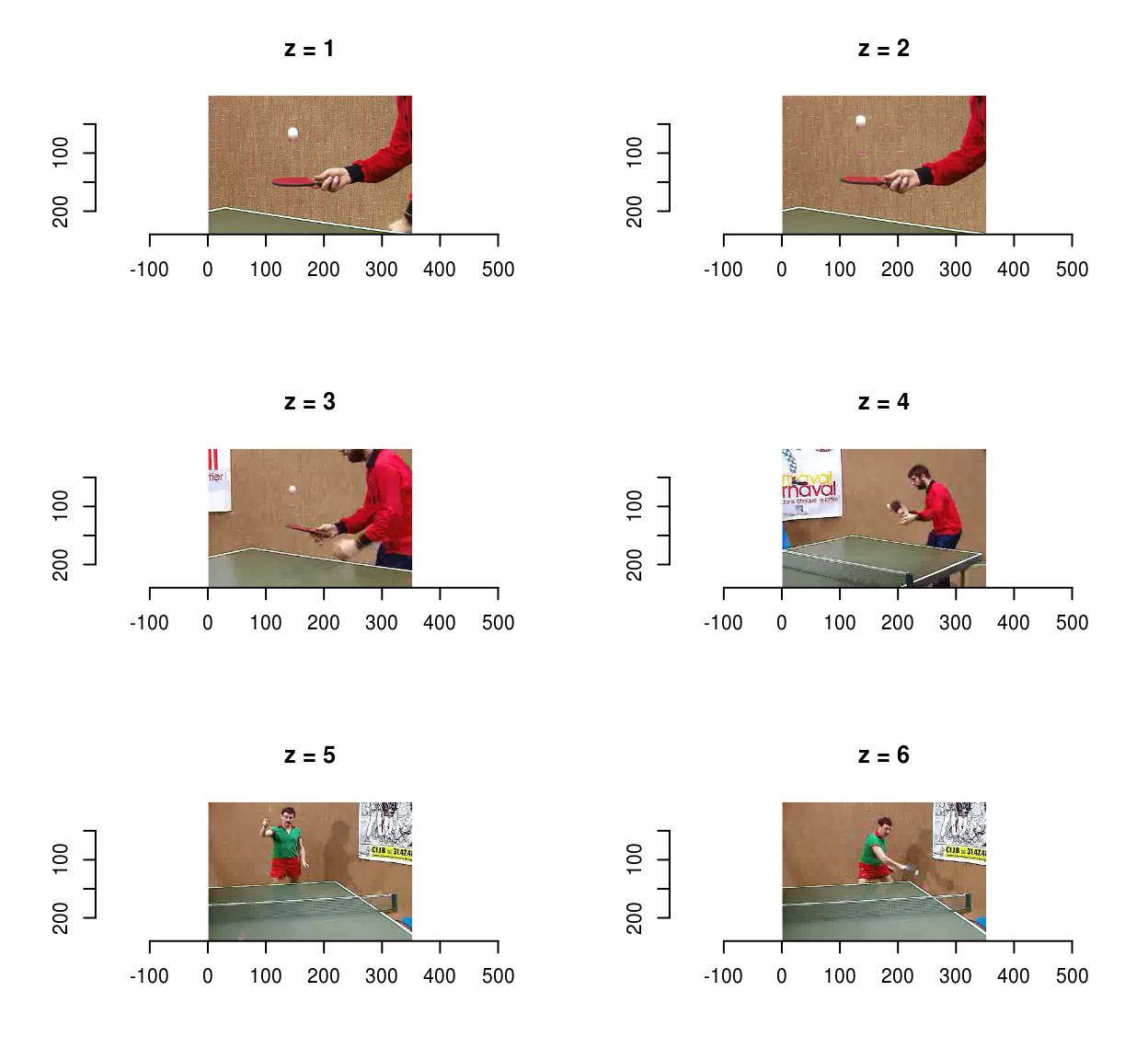

To salvage videos, use salvage.video:

            f <- tempfile(fileext=".avi") relieve.video(vid,f) load.video(f) %>% imsplit("z") %>% plot

            unlink(f)

One problem with videos is that they very quickly won't fit in memory anymore, and so you might have to bargain with them piecewise. make.video lets y'all make a video from a directory containing images representing individual frames:

            dd <- tempdir() iml <- map_il(seq(0,20,fifty=60),~ isoblur(boats,.)) #Generate file names fnames <- sprintf("%s/image-%i.png",dd,i:length(iml)) #Save each frame in a different file invisible(purrr::map2(iml,fnames,function(im,f) imager::relieve.paradigm(im,f))) f <- tempfile(fileext=".avi")  make.video(dd,f)

Displaying images and videos

To get a standard R plot utilize the plot function:

            plot(parrots)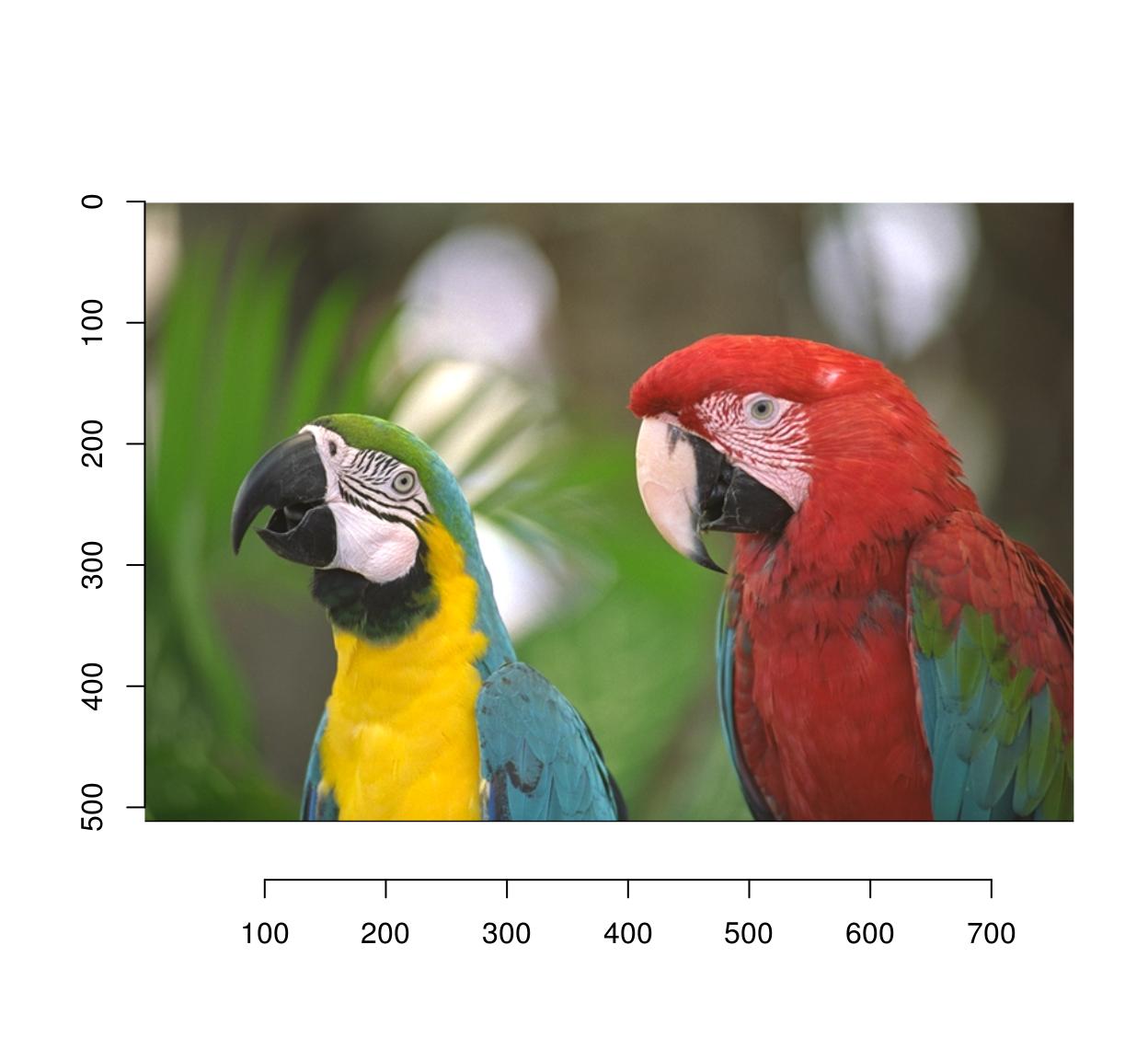

            plot(tennis,frame=1)

In addition imager provides brandish() (for images) and play() (for videos), which are much faster C++ functions for apace viewing your results. If you lot'd like to use an external viewer, you can save the paradigm to a temporary file:

            tmp <- tempfile(fileext=".png") #Open up temp. file imager::salvage.paradigm(boats,tmp) #Save image to temp. file #Call "eog [temp file]" to open in external viewer (Linux only) system2("eog",tmp) #On a mac: attempt system2("open",tmp) unlink(tmp) #Delete temp. file

How images are represented

Images are represented as 4D numeric arrays, which is consistent with CImg's storage standard (information technology is unfortunately inconsistent with other R libraries, similar spatstat, but converting betwixt representations is easy). The 4 dimensions are labelled x,y,z,c. The start two are the usual spatial dimensions, the 3rd ane volition usually correspond to depth or time, and the fourth 1 is colour. Call back the order, it volition exist used consistently in imager. If you only have grayscale images so the two extra dimensions are plain pointless, only they won't carp you much. Your objects volition all the same be officially 4 dimensional, with two abaft apartment dimensions. Pixels are stored in the following style: we browse the image beginning at the upper-left corner, along the x axis. Once we hitting the end of the scanline, we move to the next line. Once we hit the cease of the screen, we move to the adjacent frame (increasing z) and repeat the process. If we have several colour channels, and so in one case nosotros're done with the commencement colour channel we move to the adjacent one. All in all the different dimensions are represented in the x,y,z,c order. In R the object is represented equally a 4D array. Here'southward an instance with a grayscale paradigm:

            parrots <- load.example('parrots') gray.parrots <- grayscale(parrots) dim(grey.parrots)

            [1] 768 512   ane   i

and a colour paradigm:

            dim(parrots)

            [i] 768 512   1   three

and finally a video, also in colour:

            dim(tennis)

            [1] 352 240 150   iii

Coordinates

CImg uses standard epitome coordinates: the origin is at the top left corner, with the x centrality pointing right and the y axis pointing downwards. imager uses the same coordinate organization, except the origin is now (1,1) and not (0,0) (the reason beingness that R indices start at i and not at 0). The number of pixels along the ten axis is called the width, forth the y axis it's tiptop, along the z centrality information technology's depth and finally the number of colour channels is called "spectrum".

            width(parrots)

            [1] 768

            tiptop(parrots)

            [i] 512

            depth(parrots)

            [1] 1

            spectrum(parrots)

            [1] three

The cimg class

Imager uses the "cimg" class for its images. "cimg" is just a regular 4d array with an S3 class tacked on and so we tin have custom plot, impress, etc. To promote an assortment to a "cimg" object, employ equally.cimg:

            noise <- array(runif(5*five*5*3),c(5,five,v,iii)) #5x5 pixels, 5 frames, iii colours. All noise racket <- as.cimg(noise)

Y'all can treat the object as you would any other array:

            #Arithmetic sin(noise) + 3*racket

            Image. Width: 5 pix Height: five pix Depth: 5 Colour channels: 3

            #Subsetting noise[,,,1] #Offset colour aqueduct

            , , one             [,1]      [,2]      [,3]      [,4]      [,five] [1,] 0.15729737 0.1211601 0.8988929 0.4159581 0.3028848 [two,] 0.84973167 0.6274368 0.2415643 0.4966623 0.2269957 [3,] 0.54568313 0.3016971 0.2838756 0.4746036 0.2844496 [4,] 0.04863492 0.2658499 0.6029072 0.2423509 0.1071429 [5,] 0.01277593 0.5369538 0.4148199 0.4948992 0.3521130  , , 2             [,1]      [,2]      [,3]      [,iv]      [,v] [1,] 0.79095569 0.3831404 0.9740569 0.7082703 0.2716844 [2,] 0.02995088 0.4527976 0.5571453 0.3556408 0.8869119 [3,] 0.16175638 0.1366967 0.7246627 0.2537838 0.5740961 [4,] 0.40808831 0.5199738 0.3159353 0.9300932 0.5880399 [5,] 0.11933058 0.7494124 0.7374537 0.2995378 0.5914280  , , 3             [,1]      [,two]       [,3]      [,4]      [,5] [1,] 0.60391048 0.5167028 0.02420186 0.5472331 0.3797664 [2,] 0.06801864 0.5697795 0.66071426 0.9646910 0.4229982 [3,] 0.78926741 0.9300144 0.62414829 0.9306036 0.9666980 [4,] 0.27166128 0.3196066 0.03260900 0.4725431 0.7499543 [5,] 0.48957878 0.8283884 0.11846634 0.3872923 0.3950798  , , four              [,ane]      [,2]      [,three]      [,4]      [,five] [ane,] 0.002466594 0.1436853 0.9389031 0.6733791 0.1285260 [2,] 0.772557458 0.5994659 0.2597808 0.3718233 0.3210910 [three,] 0.892276678 0.7209472 0.8854790 0.7158221 0.6365918 [4,] 0.017707171 0.7006387 0.4359491 0.5040516 0.5311173 [5,] 0.897455861 0.2024645 0.4403962 0.7566717 0.3084604  , , 5             [,1]      [,ii]      [,iii]       [,4]      [,5] [1,] 0.53776992 0.4647327 0.9597835 0.01976816 0.9679417 [2,] 0.08520387 0.5630616 0.3748003 0.93281874 0.5851739 [3,] 0.08174300 0.9684200 0.6424220 0.24108078 0.6385822 [4,] 0.57478002 0.1302111 0.4727503 0.57880176 0.6190047 [5,] 0.49731932 0.1970284 0.1391678 0.60512846 0.1805122

            dim(noise[1:four,,,] )

            [i] 4 v five 3

which makes life easier if you want to use ggplot2 for plotting (see tutorial).

Yous can also convert matrices to cimg objects:

            matrix(1,10,x) %>% as.cimg

            Prototype. Width: 10 pix Height: x pix Depth: one Colour channels: 1

and vectors:

            1:9 %>% equally.cimg

            Image. Width: 3 pix Elevation: 3 pix Depth: 1 Color channels: i

which tries to guess what sort of image dimensions yous want (see tutorial).

The opposite is possible as well: if you lot accept a data.frame with columns x,y,z,cc,value, you lot can turn information technology into a cimg object:

            df <- expand.grid(ten=one:x,y=1:ten,z=1,cc=1) mutate(df,value=cos(sin(x+y)^two)) %>% every bit.cimg

            Prototype. Width: 10 pix Height: ten pix Depth: 1 Colour channels: 1

By default as.cimg.data.frame will try to gauge image size from the input. You tin can as well be specific by setting the "dims" argument explicitly:

            mutate(df,value=cos(sin(x+y)^2)) %>% equally.cimg(dims=c(10,10,one,1))

            Image. Width: 10 pix Acme: 10 pix Depth: 1 Color channels: ane

The reverse is possible as well: you can convert a cimg object to a data.frame

            caput(as.data.frame(parrots))

                          x y cc     value 1 1 1  1 0.4549020 ii 2 1  1 0.4588235 3 3 1  1 0.4705882 iv 4 ane  ane 0.4666667 v 5 1  1 0.4705882 6 6 1  1 0.4705882

or to an assortment, vector or matrix

            head(every bit.assortment(parrots))

            [one] 0.4549020 0.4588235 0.4705882 0.4666667 0.4705882 0.4705882

            head(every bit.vector(parrots))

            [1] 0.4549020 0.4588235 0.4705882 0.4666667 0.4705882 0.4705882

            grayscale(parrots) %>% every bit.matrix %>% dim

            [1] 768 512

Image lists

Many functions in imager produce lists of paradigm every bit output (see beneath). These are given the "imlist" course, e.thousand. imgradient returns:

            imgradient(parrots,"xy") %>% course

            [1] "imlist" "listing"

The imlist class comes with a few convenience functions, for example:

            imgradient(parrots,"xy") %>% plot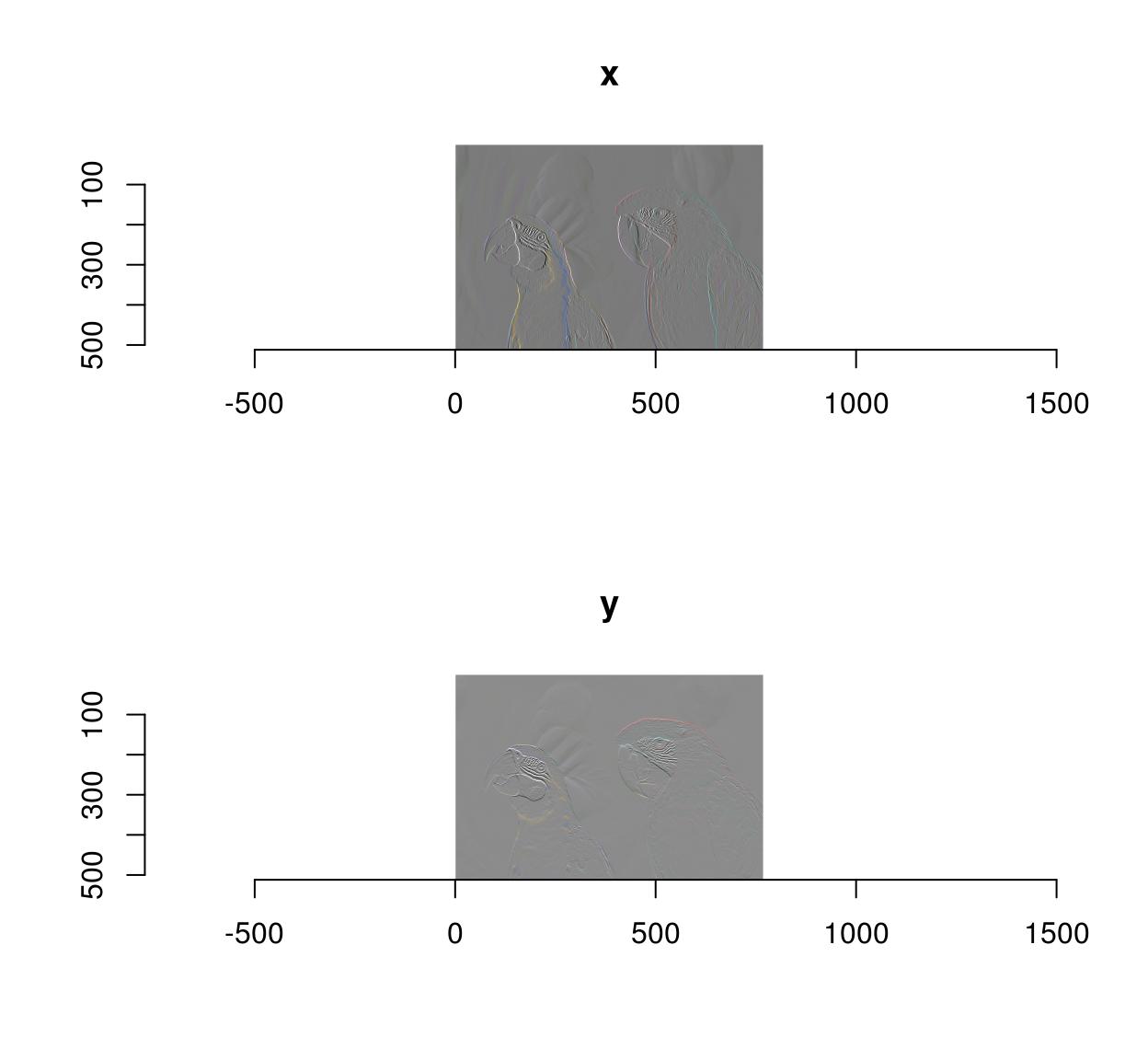

and:

            imgradient(parrots,"xy") %>% as.data.frame %>% caput

                          im x y cc        value 1  x 1 i  i  0.001386484 ii  10 2 1  1  0.006120236 3  x 3 1  1  0.002198667 4  x four 1  1 -0.001722901 five  ten 5 i  1  0.002535085 6  10 6 one  1 -0.001287949

where the "im" column indexes the image in the list.

To make an image list straight, use "imlist" or as.imlist

            imlist(a=parrots,b=3*parrots)

            Paradigm list of size two

            listing(a=parrots,b=iii*parrots) %>% as.imlist

            Image list of size 2

Pixel sets (pixsets)

Some other important datatype in imager is the pixel set (AKA pixset, introduced in imager v0.forty). A pixset is a set of pixels, represented equally a binary image, and that's what you lot become when you lot examination properties on images, east.g.:

            grayscale(parrots) > .8

            Pixel set of size 21353. Width: 768 pix Height: 512 pix Depth: i Colour channels: 1

Internally a pixset is just a assortment of logicals, then information technology's no unlike from what you'd get from running a test on a vector, e.grand.:

            i:4  >= 2

            [1] Faux  Truthful  True  Truthful

Compared to logical arrays, however, pixsets come with many convenience functions, for plotting, splitting, morphological operations, etc.

As an example, the following bit of code generates random shapes by filtering & thresholding a random paradigm, splitting it into continued components, and removing the smaller ones:

            set.seed(ane) imnoise(100,100) %>% isoblur(three) %>%     threshold(0) %>% split_connected %>%     purrr::keep(~ sum(.) > 200) %>% plot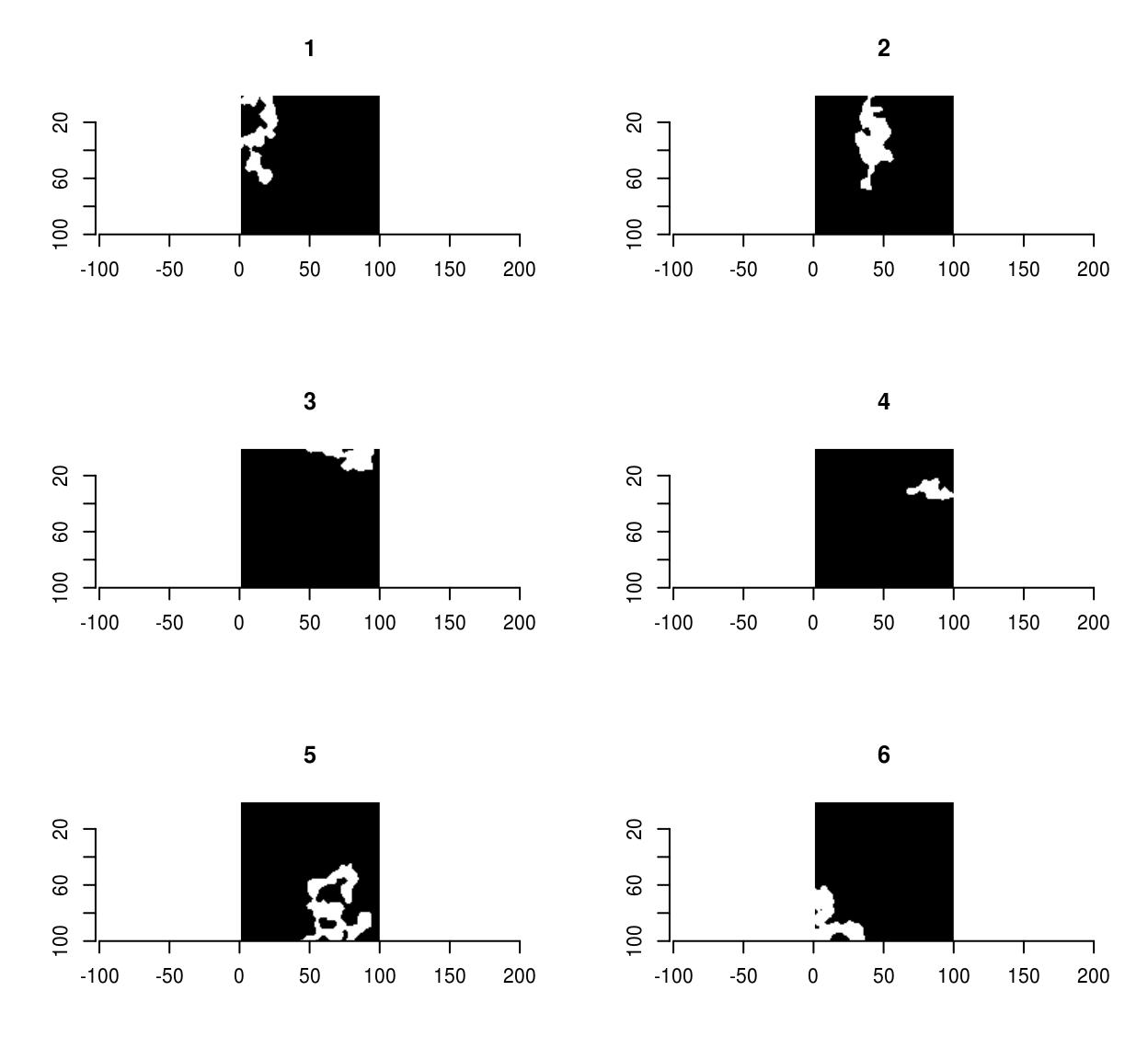

Pixsets are covered elsewhere, in the vignette vignette('pixsets'), and in the morphology tutorial.

Splitting and concatenating images

1 ofttimes needs to perform carve up computations on each aqueduct of an image, or on each frame, each line, etc. This tin be achieved using a loop or more conveniently using imsplit:

            imsplit(parrots,"c") #A list with three elements corresponding to the three channels

            Image list of size iii

            imsplit(parrots,"c") %>% laply(mean) #Mean pixel value in each channel

            [ane] 0.4771064 0.4297881 0.2972314

            imsplit(parrots,"x") %>% laply(mean) %>% head #Mean pixel value in each line (across all channels)

            [1] 0.3666948 0.3682700 0.3697508 0.3705525 0.3707925 0.3708410

            ##For a more than modern version, using purrr imsplit(parrots,"c") %>% purrr::map_dbl(mean) #Mean pixel value in each channel

                          c = 1     c = two     c = 3  0.4771064 0.4297881 0.2972314

imsplit contains an additional argument, called "nb". When "nb" is positive imsplit cuts the image into "nb" chunks, along the axis "axis":

            imsplit(parrots,"10",iv) %>% plot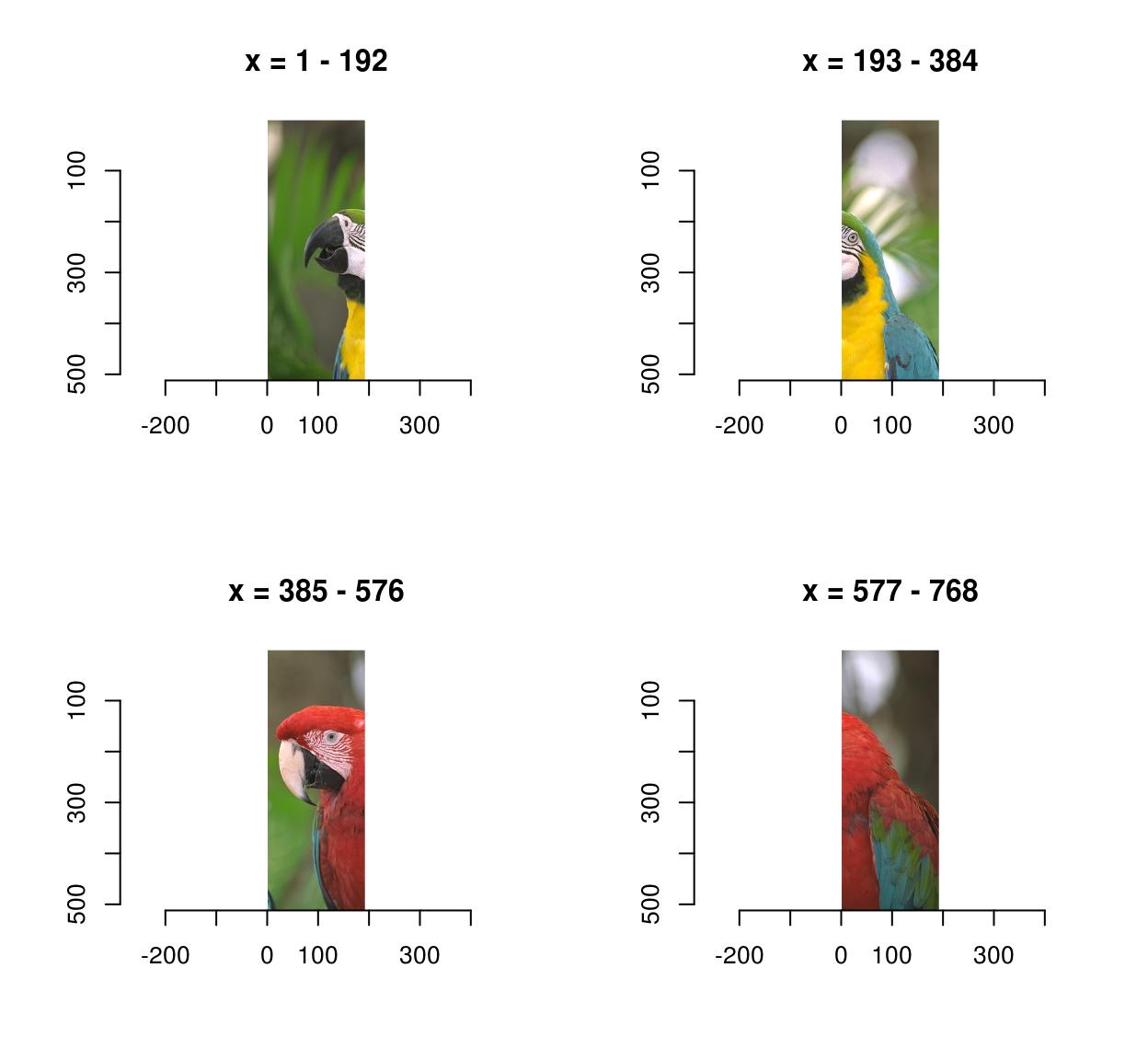

            imsplit(parrots,"y",3) %>% plot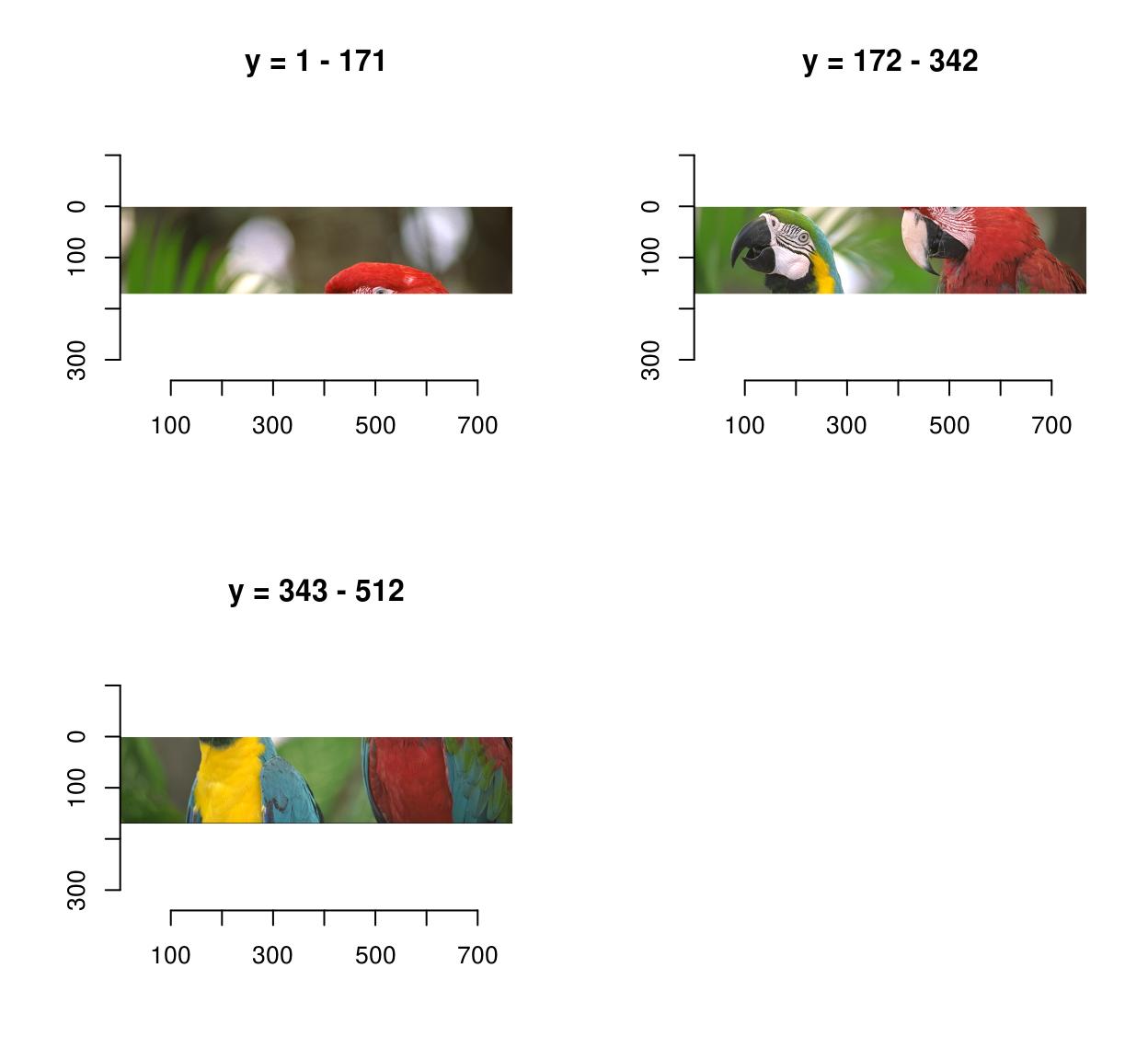

When "nb" is negative, "nb" pixels defines the chunk size:

            imsplit(parrots,"10",-250) %>% plot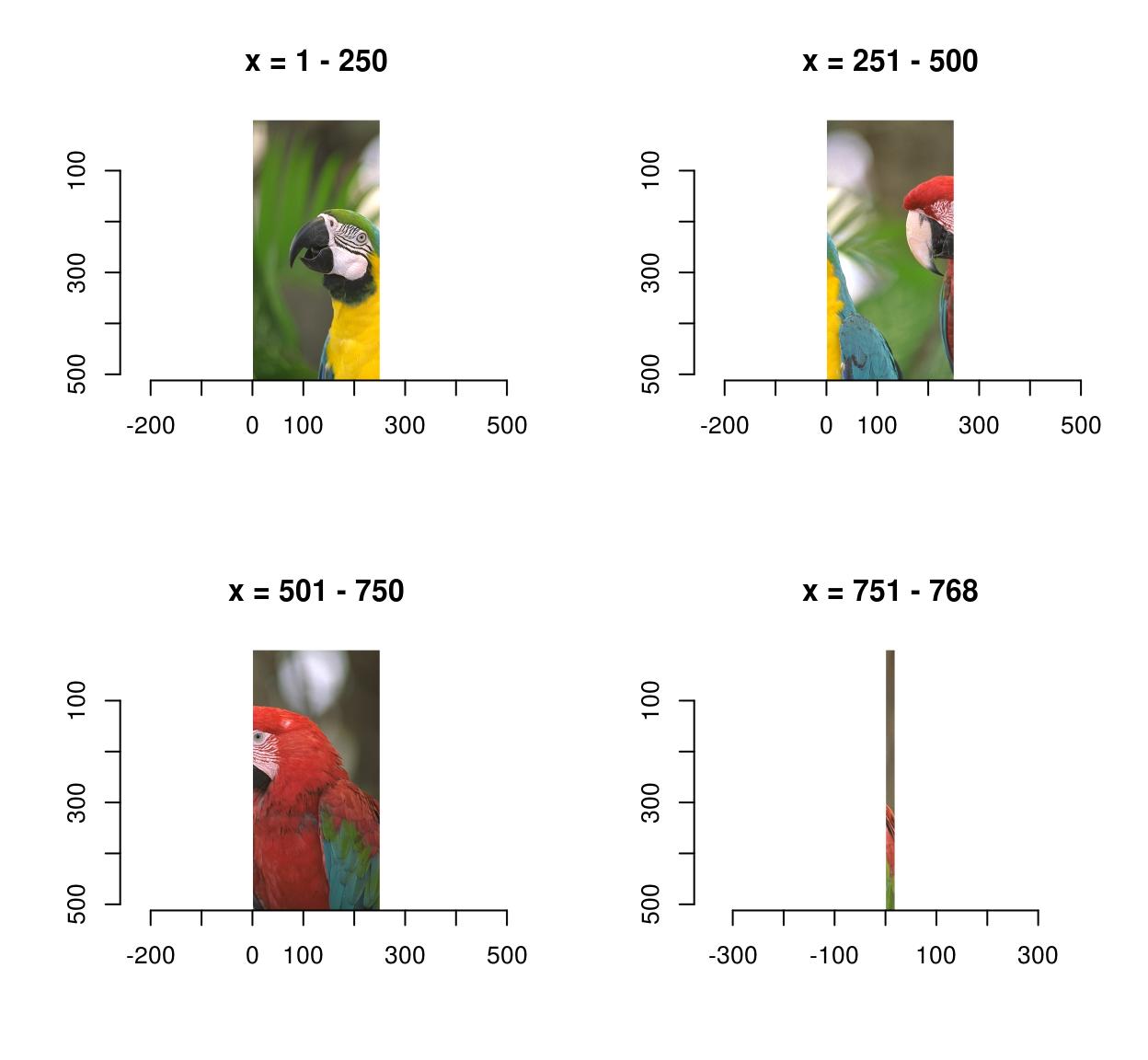

That last panel looks crummy because information technology's a long-and-sparse paradigm stretched into a square.

The inverse functioning to imsplit is chosen imappend: it takes a list of images and concatenates them along the dimension of your choice.

            #Sample functions and plow them into separate R,Chiliad,B channels R <- equally.cimg(office(ten,y) sin(cos(3*x*y)),100,100) G <- as.cimg(function(10,y) sin(cos(3*x*y + pi/2)),100,100) B <- equally.cimg(part(x,y) exp(-.03*ten),100,100) trippy <- imappend(list(R,Yard,B),"c") #Demark the three channels into one image plot(trippy)

Divide, use, combine

Ofttimes what i wants to do is to separate the image along a sure axis (e.grand. colour), apply a transformation separately and recombine the result. iiply does that:

            iiply(parrots,"c",function(5) v/max(five))  %>% plot

            #Same thing merely longer: #imsplit(parrots,"c") %>% llply(role(5) five/max(v) %>% imappend("c") %>% plot

The code above separates color channels, applies a normalisation and recombines the effect into an image. Following the same convention used by plyr, imager besides defines ilply (which splits, applies and returns a listing), idply (which splits, applies and returns a data.frame) and liply (which applies, combines and returns an paradigm).

Another way to combine after a dissever is to take the mean result, or a production, etc (the same way layers are combined in an image editing programme). You lot can do this using shortcuts divers past imager:

            imsplit(parrots,"c") %>% add %>% plot(main="Calculation colour channels")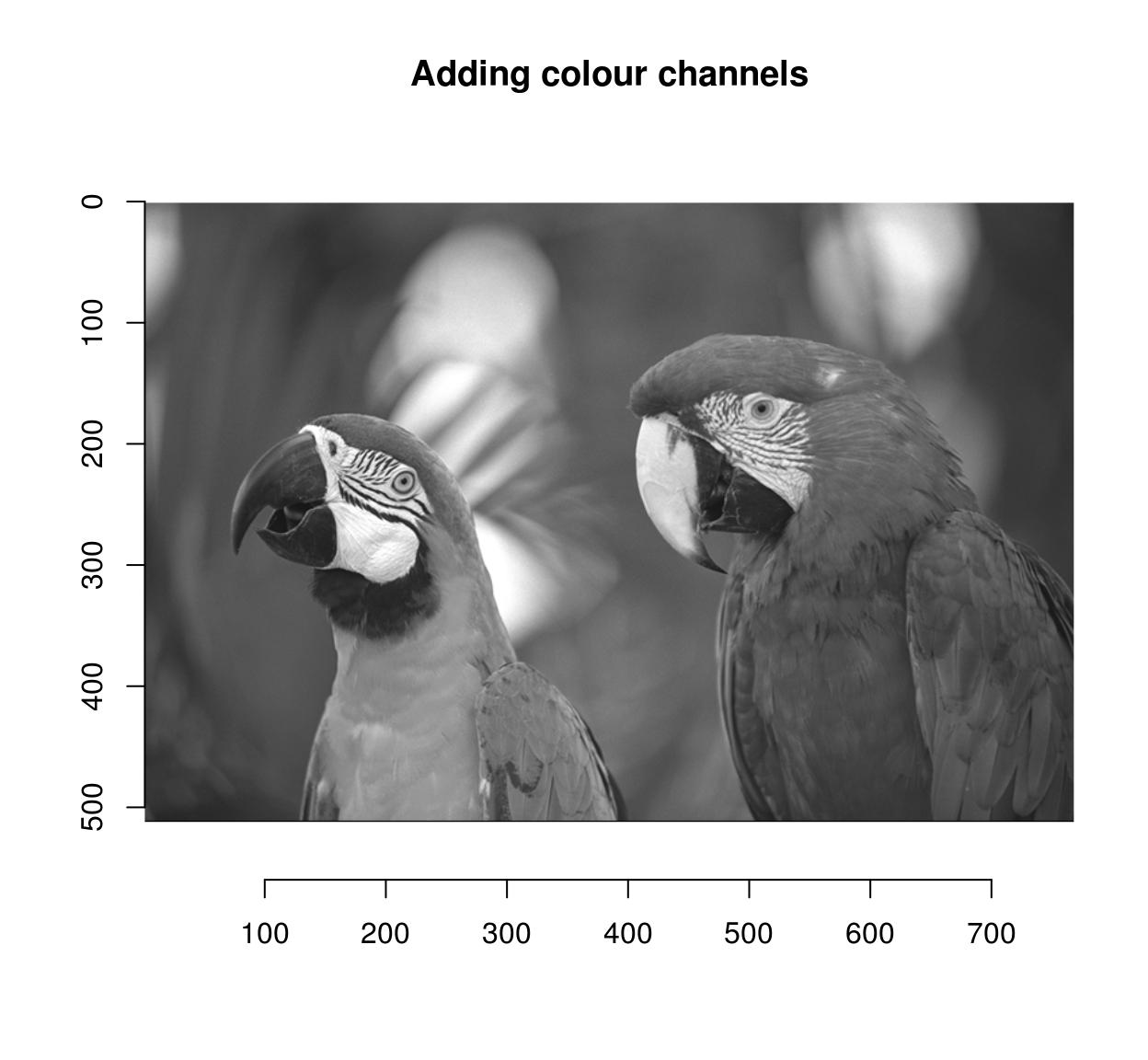

            #Apply different levels of blur on the same image blur.layers <- map_il(seq(1,15,50=v),~ isoblur(parrots,.))  blur.layers %>% parmin %>% plot(main="Min across blur levels")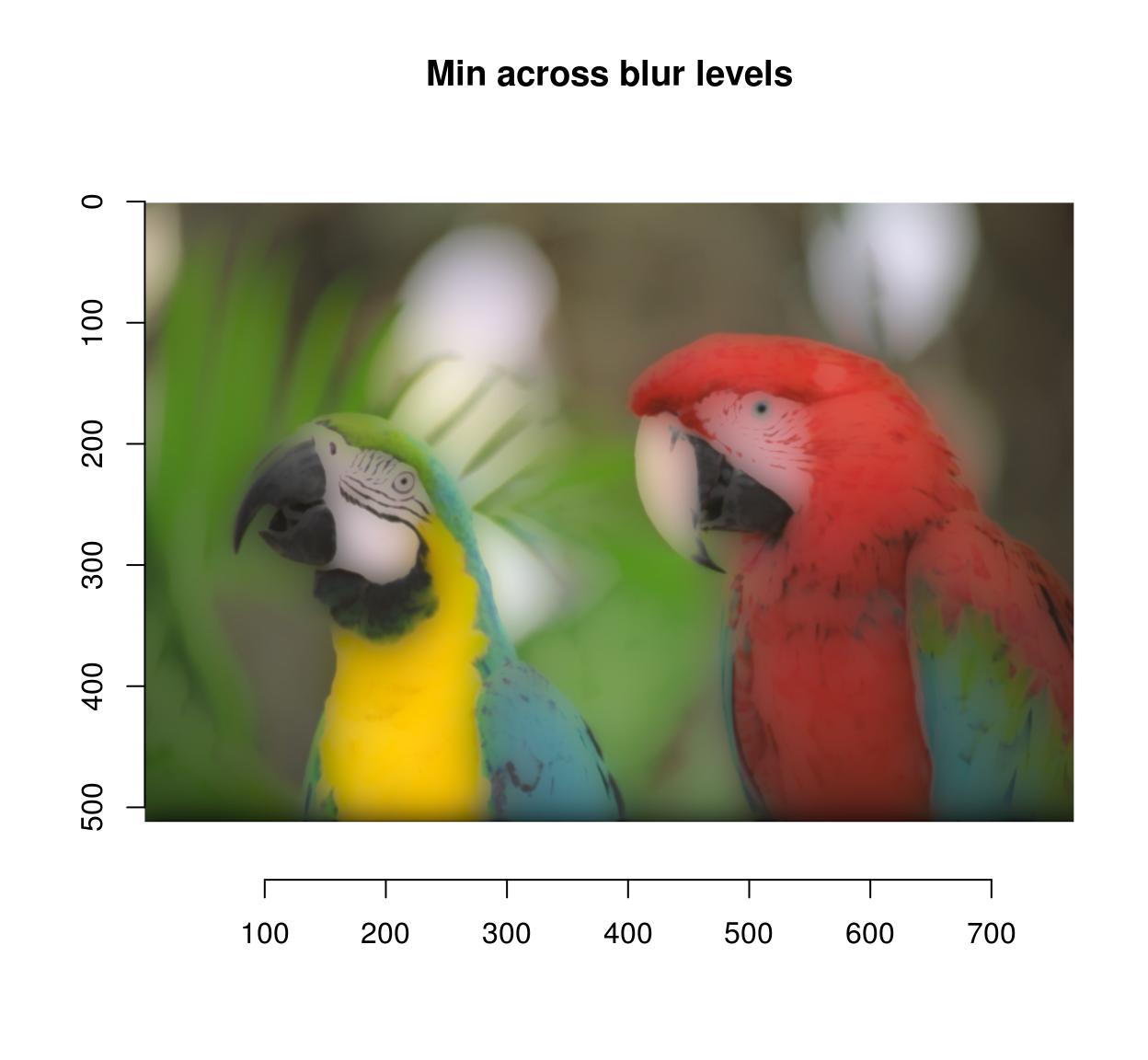

            blur.layers %>% parmax %>% plot(main="Max beyond blur levels")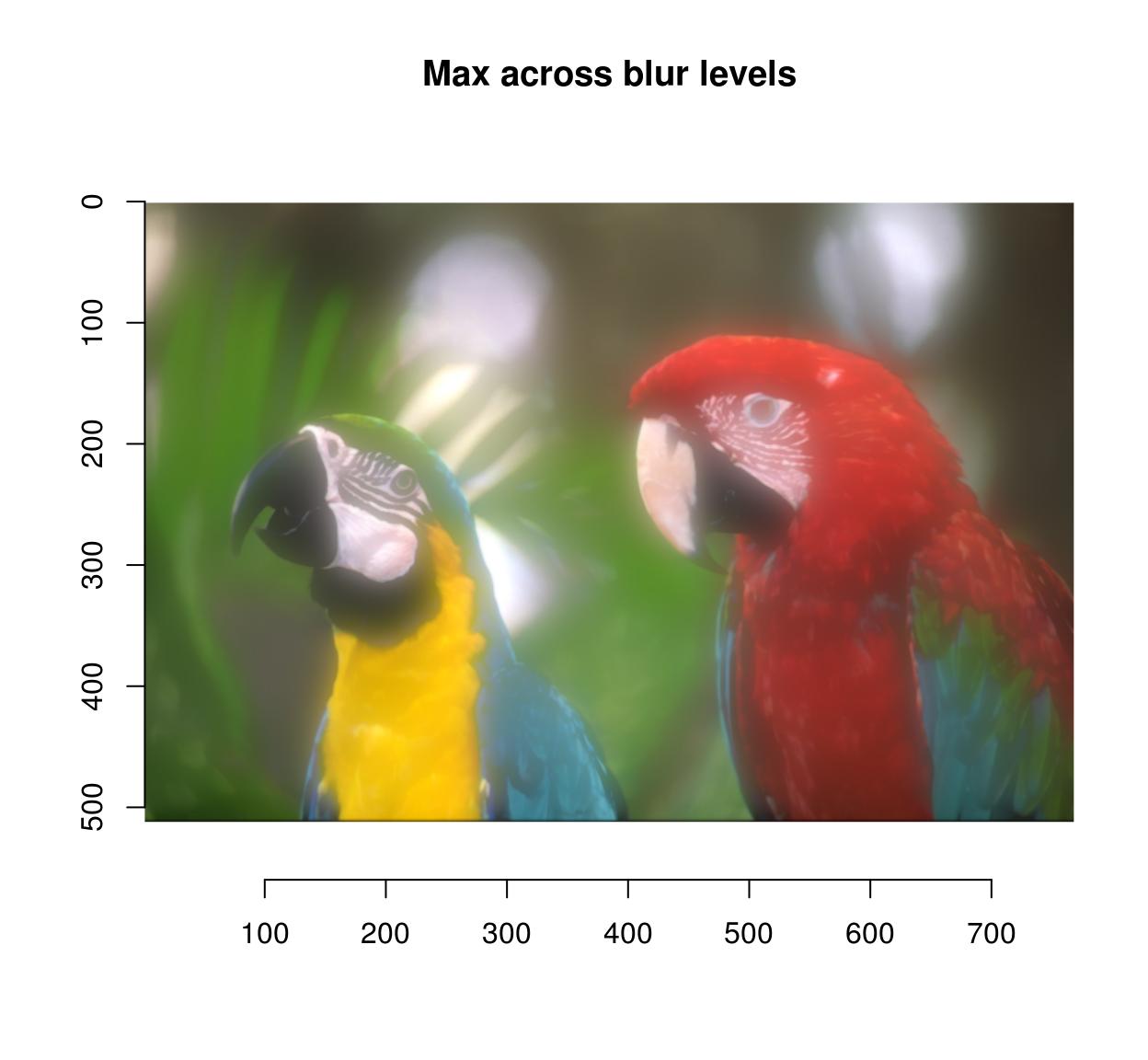

            blur.layers %>% average %>% plot(main="Average across blur levels")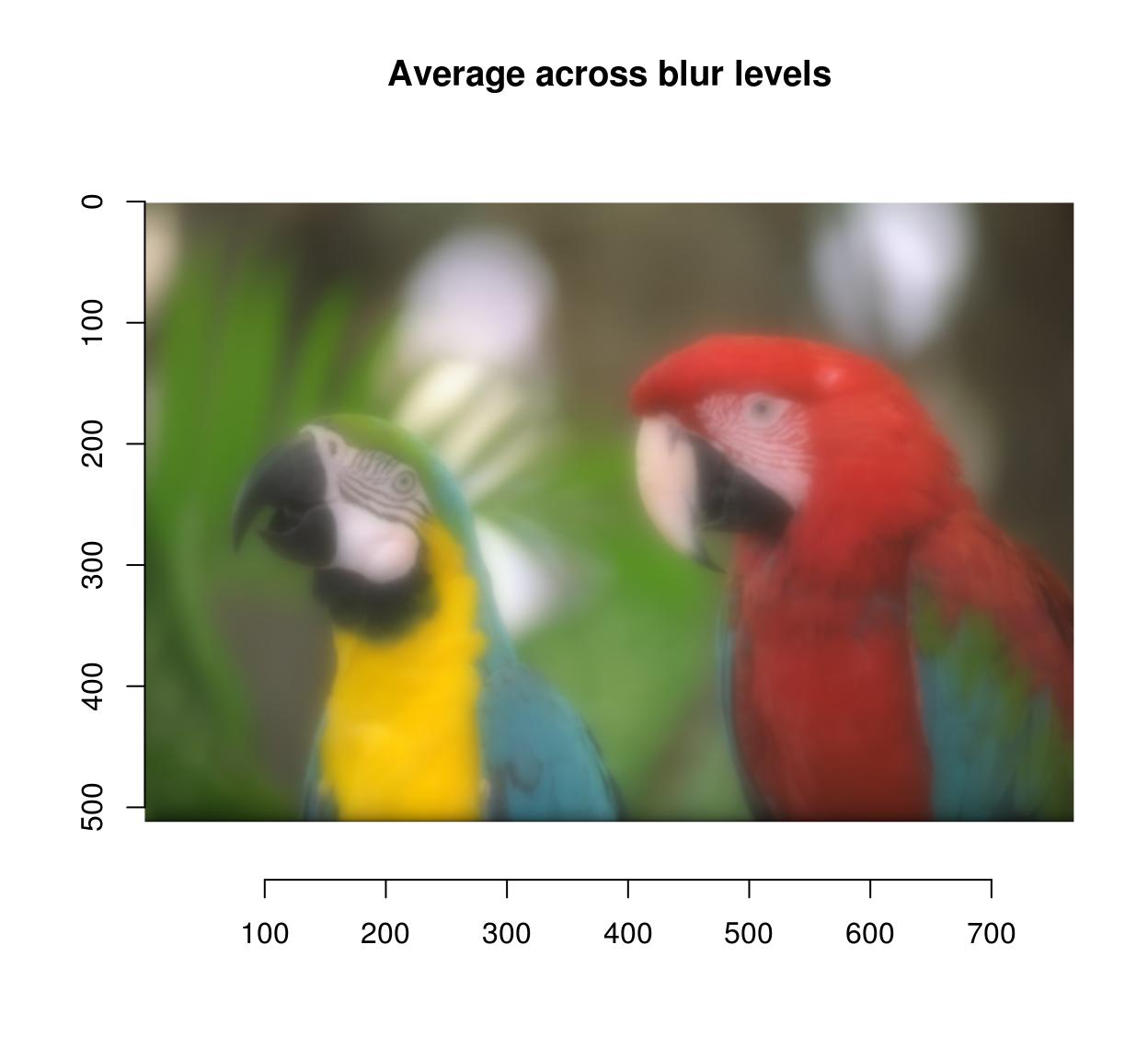

            blur.layers %>% parmed %>% plot(main="Median across blur levels")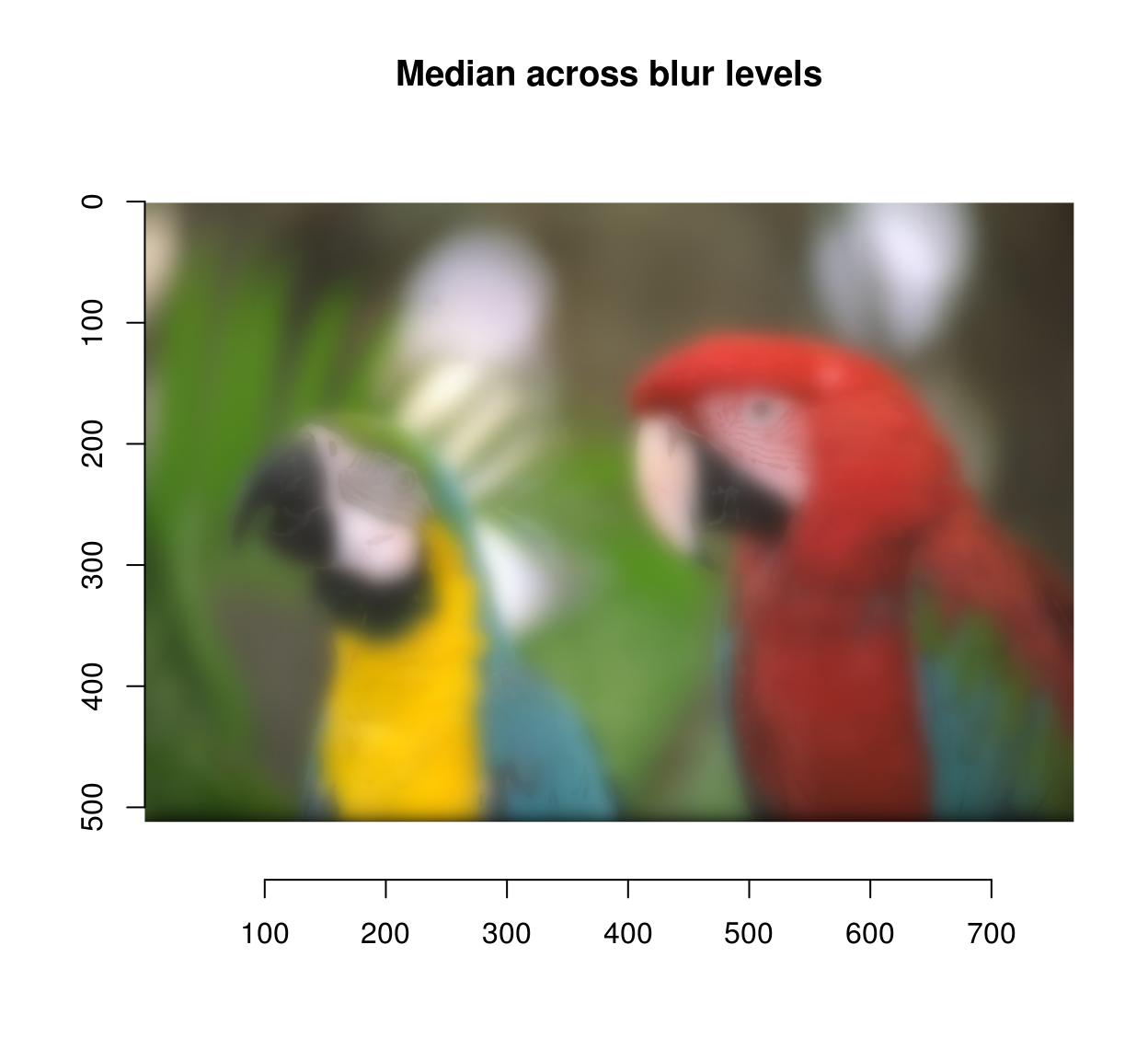

Sub-images, pixel neighbourhoods, etc.

If y'all need to select a office of an epitome, you can utilize imsub, which is best explained past example:

            imsub(parrots,x < thirty) #Only the beginning 30 rows

            Prototype. Width: 29 pix Elevation: 512 pix Depth: one Colour channels: 3

            imsub(parrots,y < thirty) #Only the first thirty rows

            Prototype. Width: 768 pix Height: 29 pix Depth: 1 Colour channels: 3

            imsub(parrots,x < 30,y < 30) #First thirty columns and rows

            Prototype. Width: 29 pix Height: 29 pix Depth: ane Colour channels: three

            imsub(parrots, sqrt(x) > 8) #Tin can use arbitrary expressions

            Image. Width: 704 pix Elevation: 512 pix Depth: 1 Color channels: 3

            imsub(parrots,10 > acme/2,y > width/2)  #height and width are defined based on the epitome

            Paradigm. Width: 512 pix Meridian: 128 pix Depth: 1 Color channels: iii

            imsub(parrots,cc==1) #Colour centrality is "cc" not "c" here because "c" is an of import R role

            Epitome. Width: 768 pix Height: 512 pix Depth: 1 Colour channels: 1

Pixel neighbourhoods (for example, all nearest neighbours of pixel (10,y,z)) can be selected using stencils. Run across ?get.stencil and the vignette on natural image statistics for more.

If y'all demand to admission a specific colour aqueduct, utilise any of the following:

            R(parrots)

            Image. Width: 768 pix Height: 512 pix Depth: 1 Colour channels: 1

            One thousand(parrots)

            Image. Width: 768 pix Top: 512 pix Depth: 1 Color channels: 1

            B(parrots)

            Paradigm. Width: 768 pix Top: 512 pix Depth: i Color channels: i

            #R(parrots) is equivalent to channel(parrots,one)  #Set all channels to 0 except scarlet parrots.cp <- load.instance("parrots") G(parrots.cp) <- 0 B(parrots.cp) <- 0 plot(parrots.cp)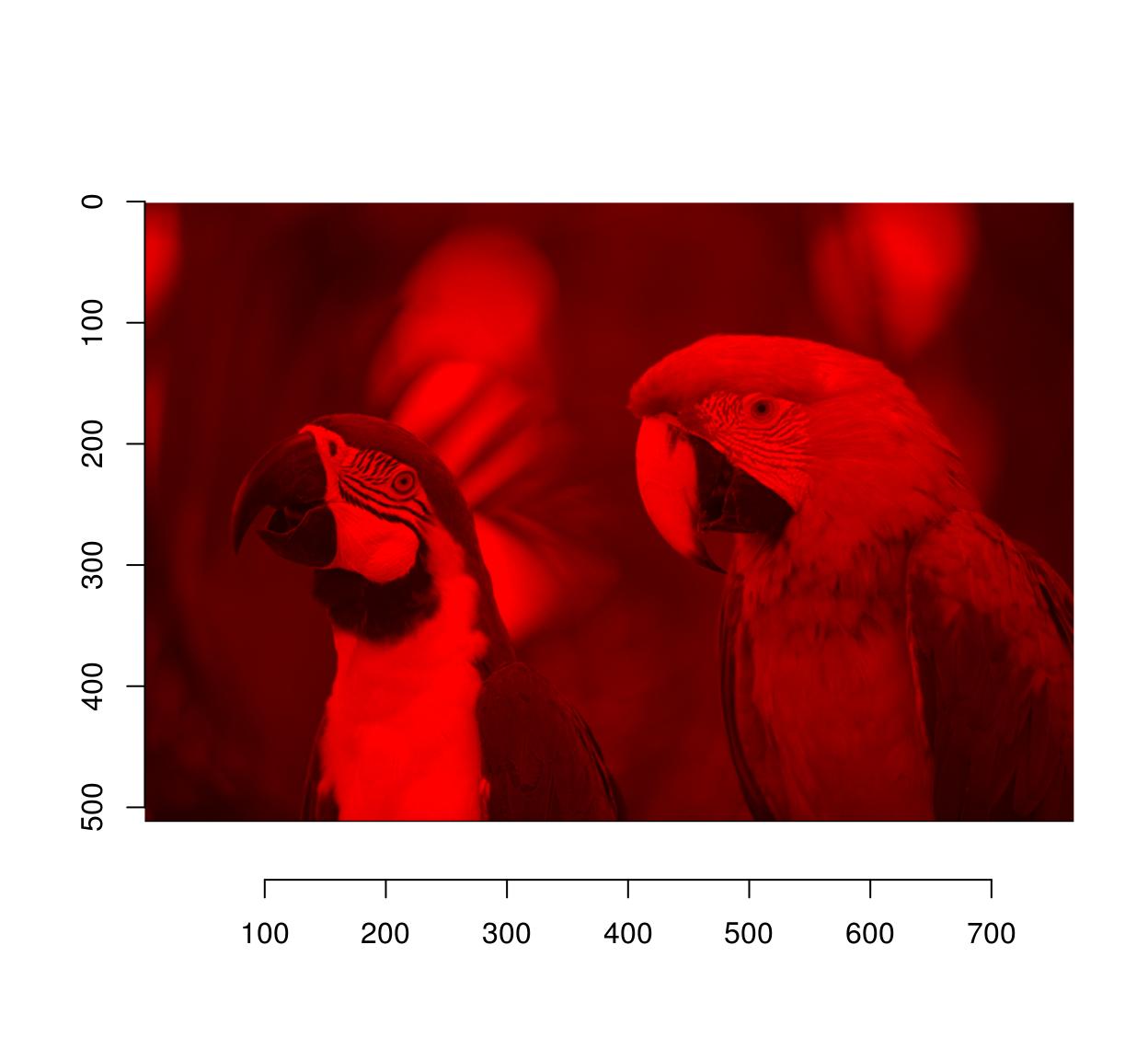

If you need to access a specific frame, utilise frame:

            frame(tennis,ane)

            Epitome. Width: 352 pix Height: 240 pix Depth: 1 Colour channels: three

            #Blur frame 1 frame(tennis,1) <- isoblur(frame(tennis,1),10)

If you need pixel values along rows and columns use:

            imrow(R(parrots),10) %>% plot(main="Cherry-red aqueduct along 10th row",type="fifty")

            imcol(B(parrots),10) %>% plot(principal="Blue channel forth 10th line",blazon="50")

Private pixels tin exist accessed using at and color.at:

            at(parrots,x=20,y=20,cc=1:3)

            [1] 0.6313725 0.5882353 0.4941176

            colour.at(parrots,x=20,y=20)

            [1] 0.6313725 0.5882353 0.4941176

Finally all of this is available under the familiar grade of the array subset operator, which tries to save yous some typing by filling in flat dimensions:

            im <- imfill(iv,iv) dim(im) #4 dimensional, merely the last ii dimensions are singletons

            [1] 4 4 1 1

            im[,1,,] <- 1:four #Assignment the standard fashion im[,ane] <- 1:four #Shortcut

Denoising

Denoising can exist performed using basic filters that boilerplate over space:

            birds <- load.image(organisation.file('extdata/Leonardo_Birds.jpg',package='imager')) birds.noisy <- (birds + .5*rnorm(prod(dim(birds))))  layout(t(1:2)) plot(birds.noisy,chief="Original") isoblur(birds.noisy,5) %>% plot(main="Blurred")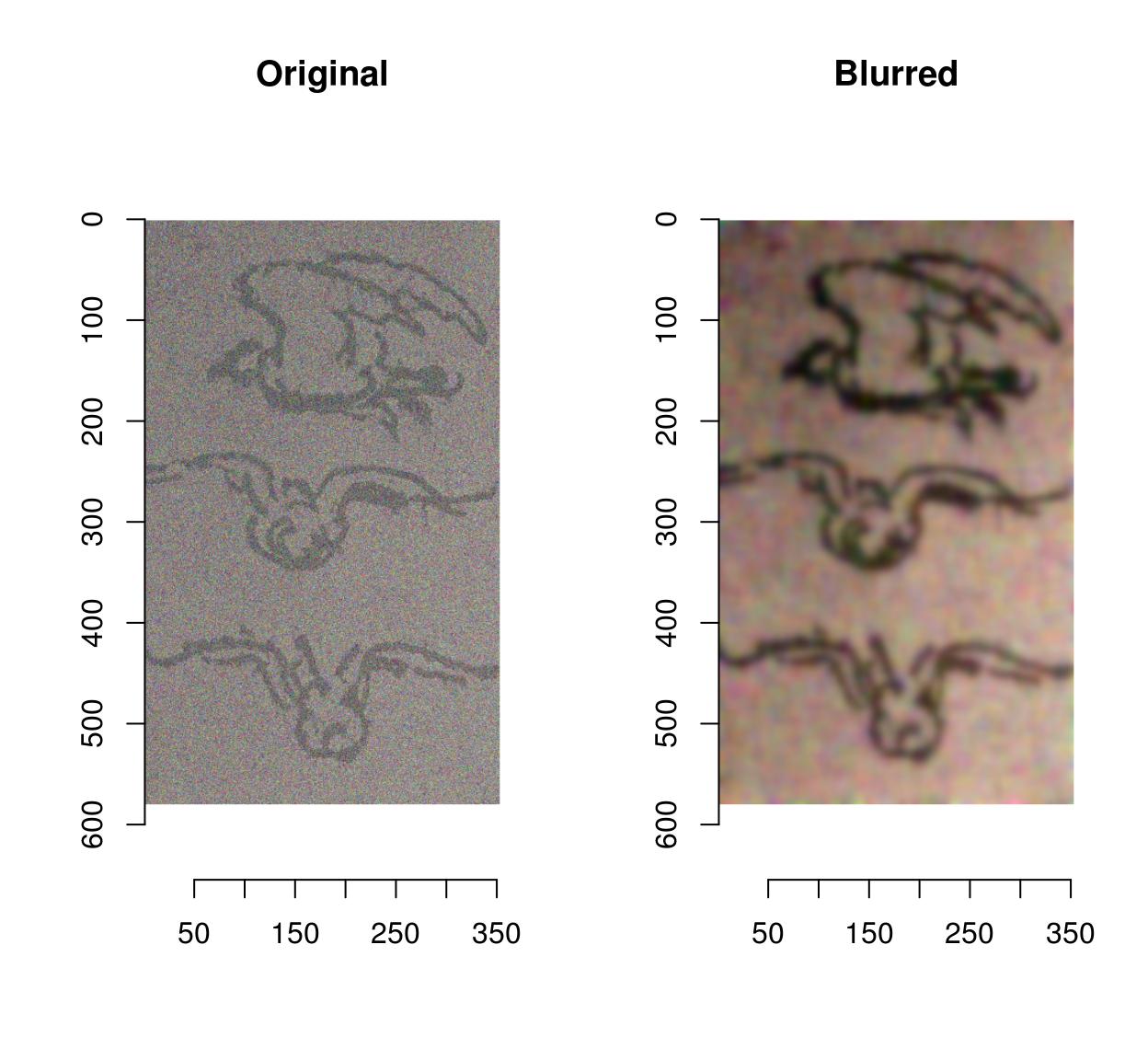

Blurring removes some of the noise but as well blurs away the contours. CImg provides an anisotropic blur that does not have that problem:

            layout(t(1:two)) plot(birds.noisy,primary="Original") blur_anisotropic(birds.noisy,ampl=1e3,sharp=.3) %>% plot(main="Blurred (anisotropic)")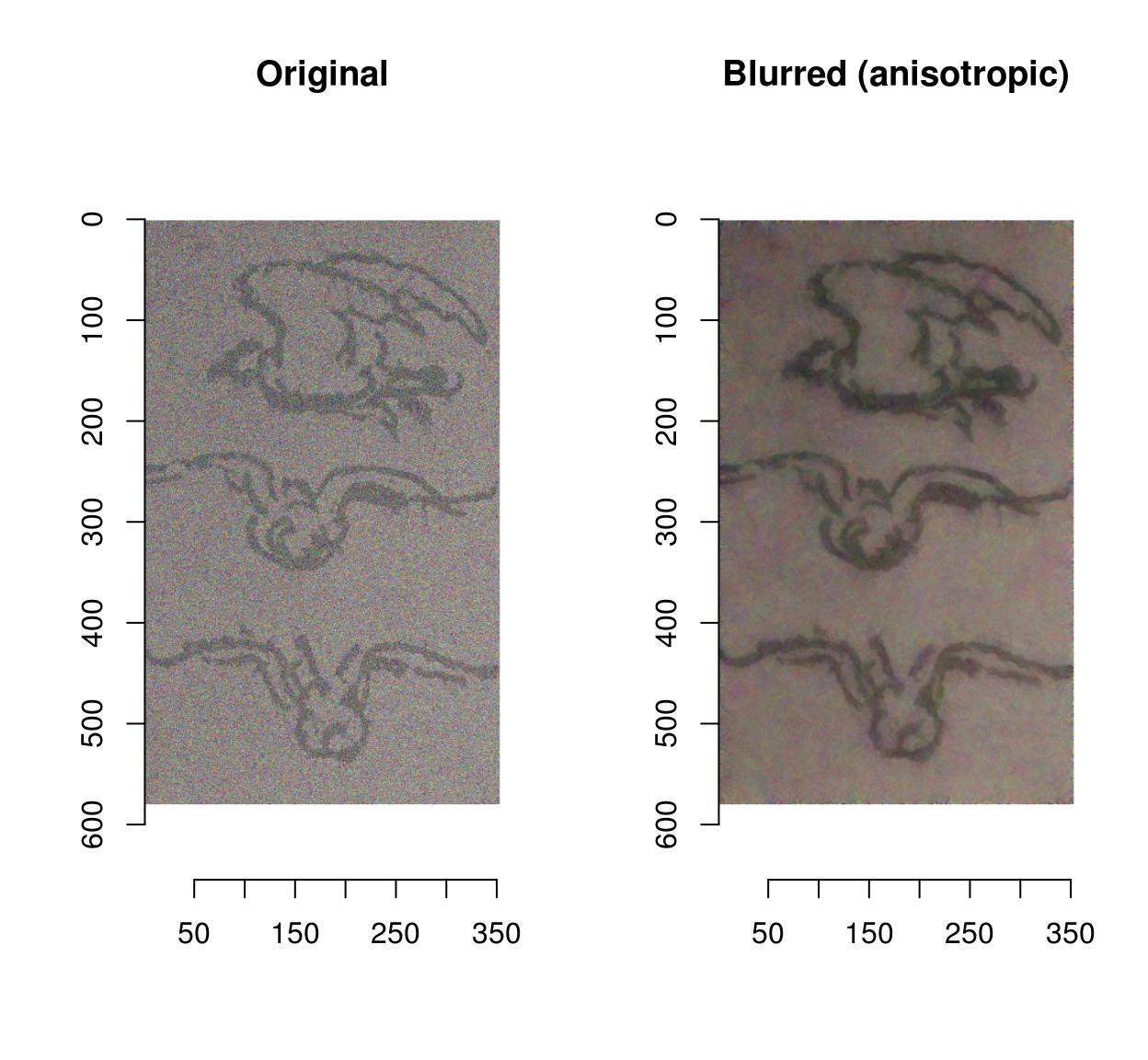

Color spaces

To catechumen from RGB to HSL/HSV/HSI/YUV/YCbCR, run RGBto[…], as in the following example:

            parrots.hsl <- RGBtoHSL(parrots) chan <- channels(parrots.hsl) #Excerpt the channels as a list of images names(chan) <- c("H","S","L") #Plot layout(matrix(1:3,one,three)) l_ply(names(chan),function(nm) plot(chan[[nm]],main=nm))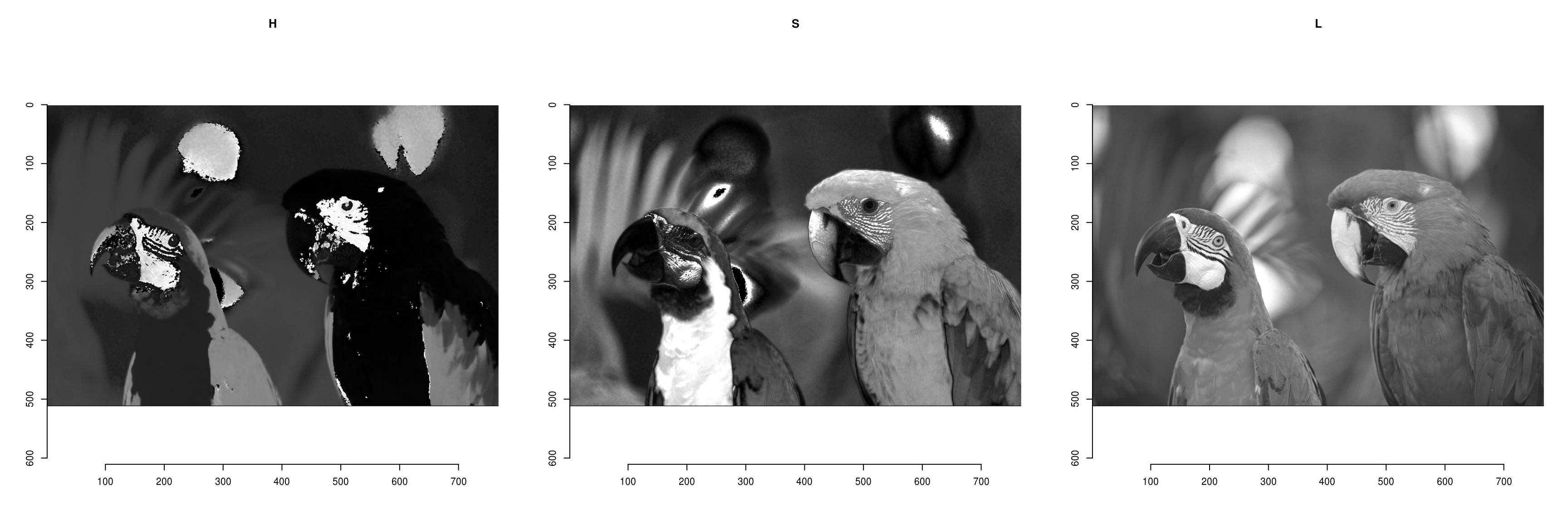

The contrary performance is done by running […]toRGB. Note that all display functions assume that your image is in RGB.

            YUVtoRGB(trippy) %>% plot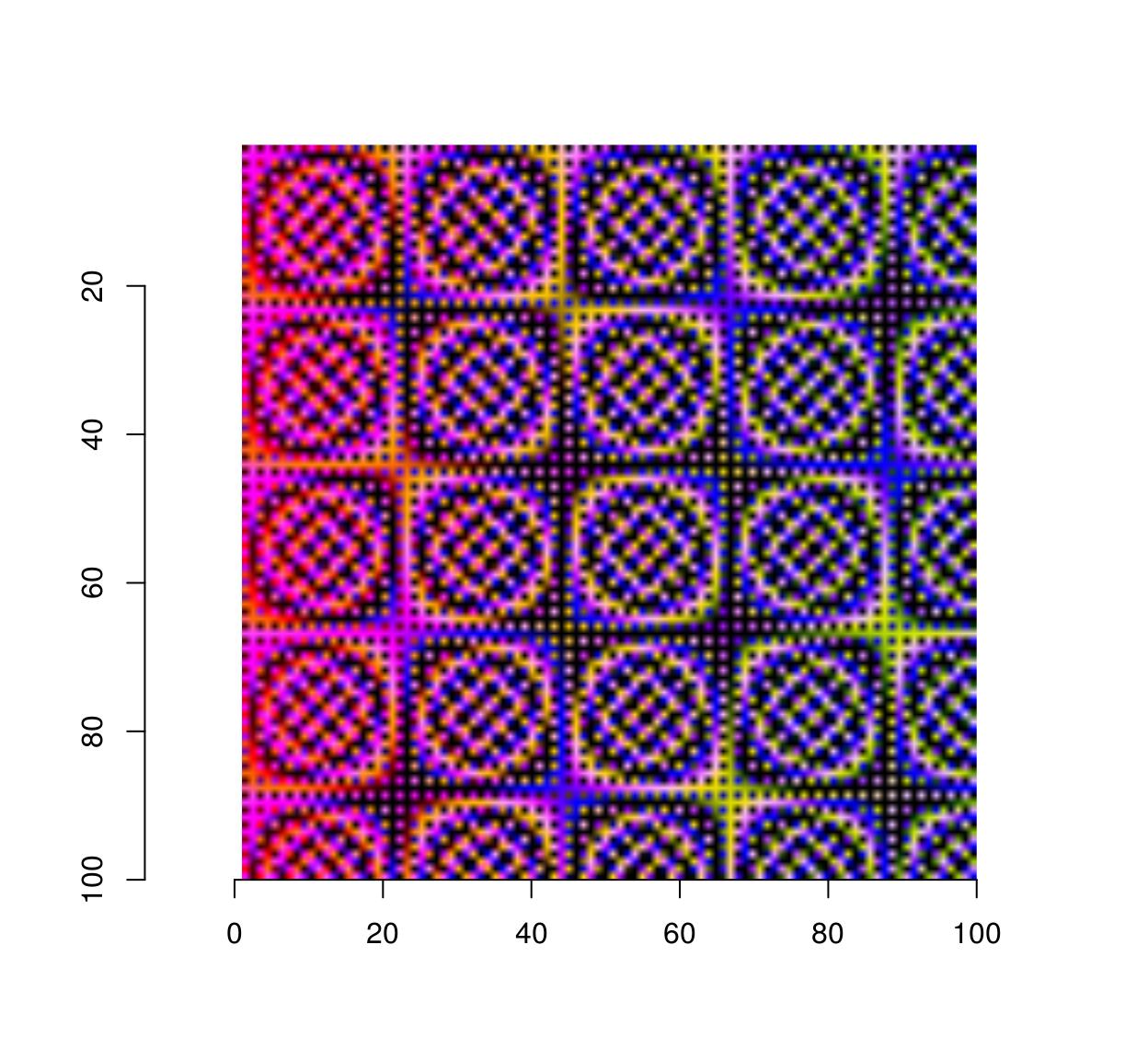

If yous have a colour image, you convert it to grayscale using the grayscale part. If you have a grayscale image, add together colour channels using add together.colour:

            grayscale(parrots) %>% spectrum

            [i] 1

            #Image has only ane channel (luminance)  grayscale(parrots) %>% add.colour %>% spectrum

            [1] 3

            #Paradigm is nevertheless in gray tones but has R,Grand,B channels

Resizing, rotation, etc.

Functions for resizing and rotation should exist fairly intuitive:

            thmb <- resize(parrots,circular(width(parrots)/10),round(height(parrots)/x)) plot(thmb,principal="Thumbnail") #Pixellated parrots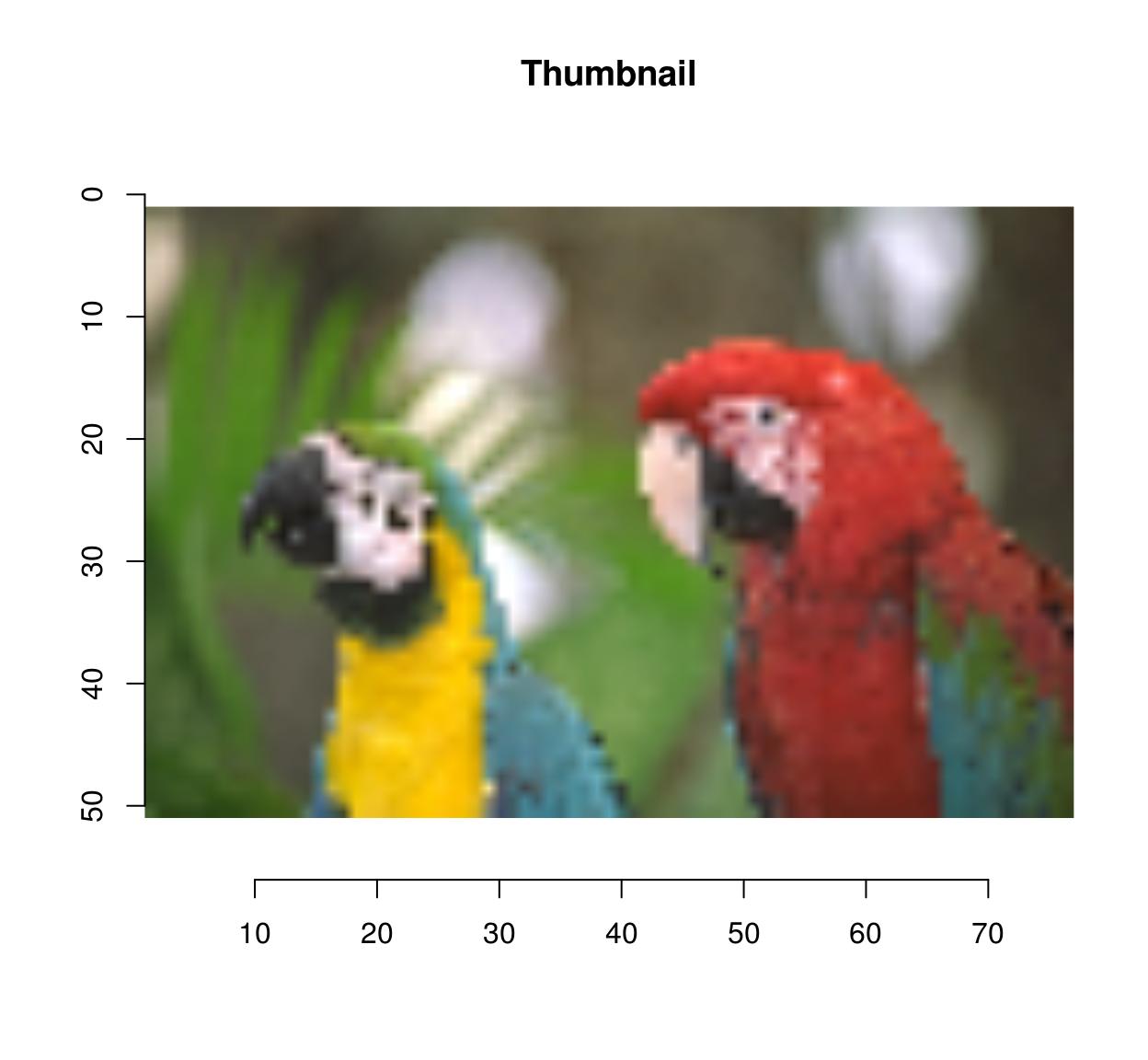

            #Same every bit above: negative arguments are interpreted as percentages thmb <- resize(parrots,-x,-10)  imrotate(parrots,30) %>% plot(main="Rotating")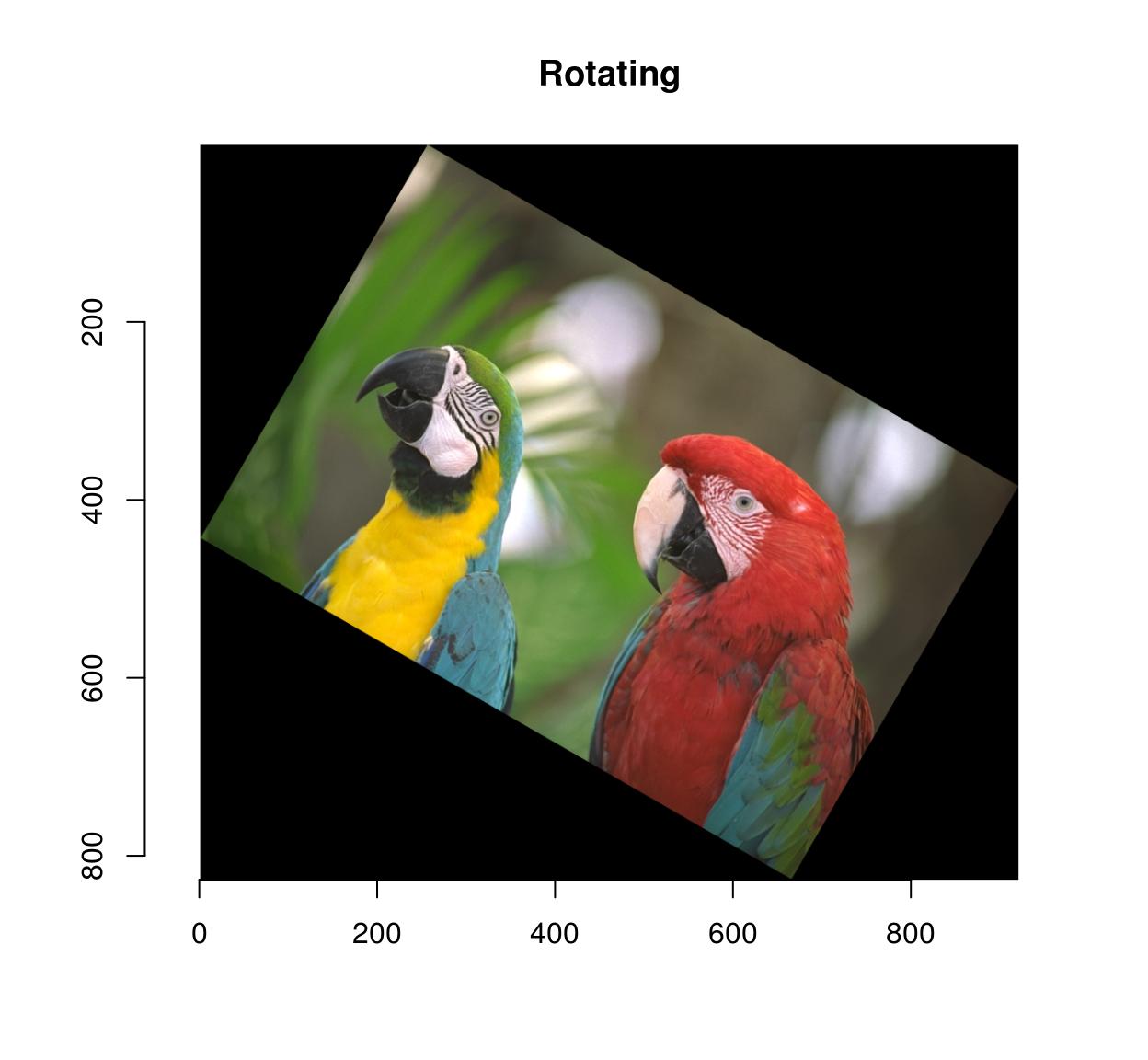

            imshift(parrots,40,20) %>% plot(primary="Shifting")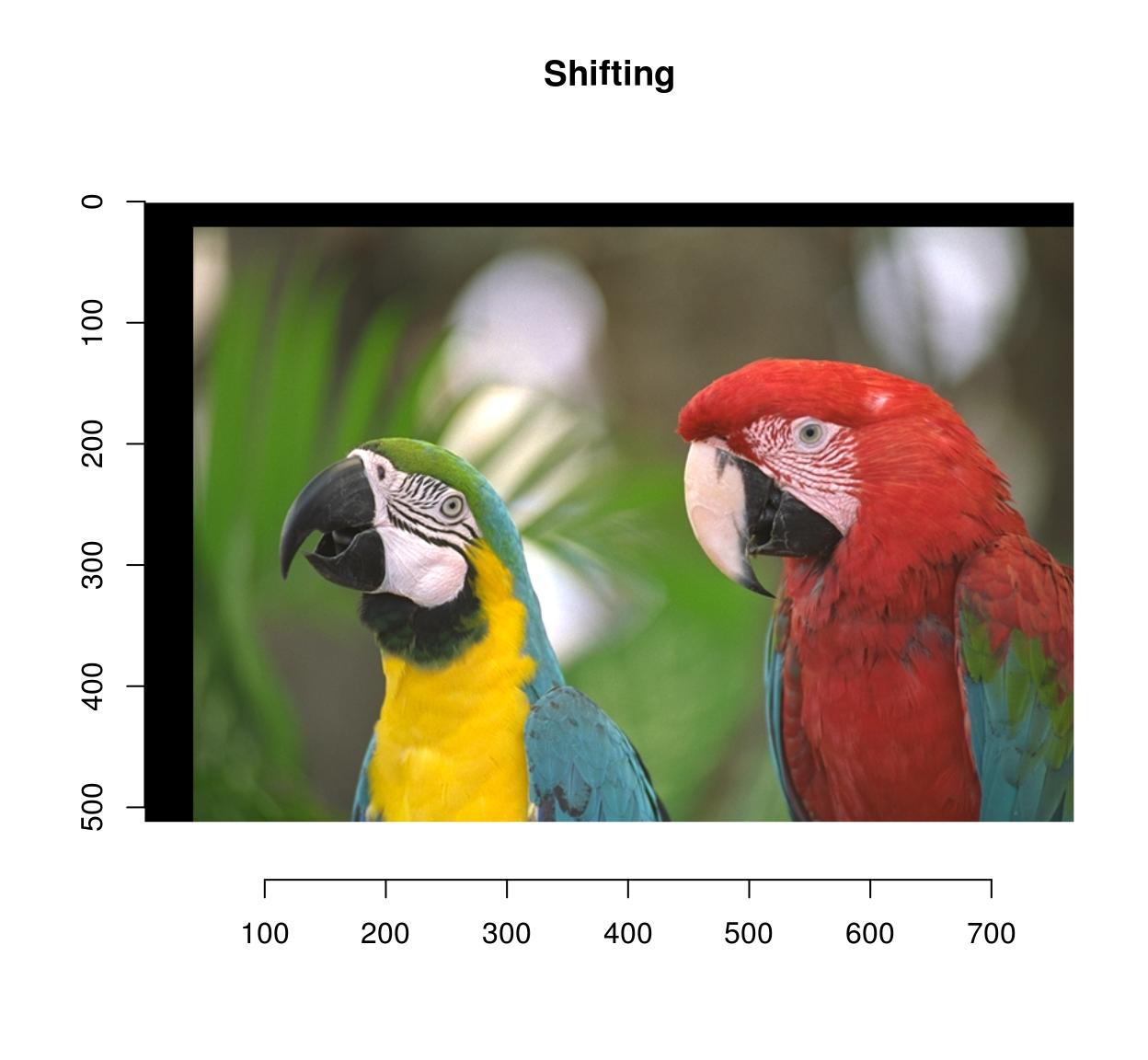

            imshift(parrots,100,100,boundary=1) %>% plot(main="Shifting (Neumann boundaries)")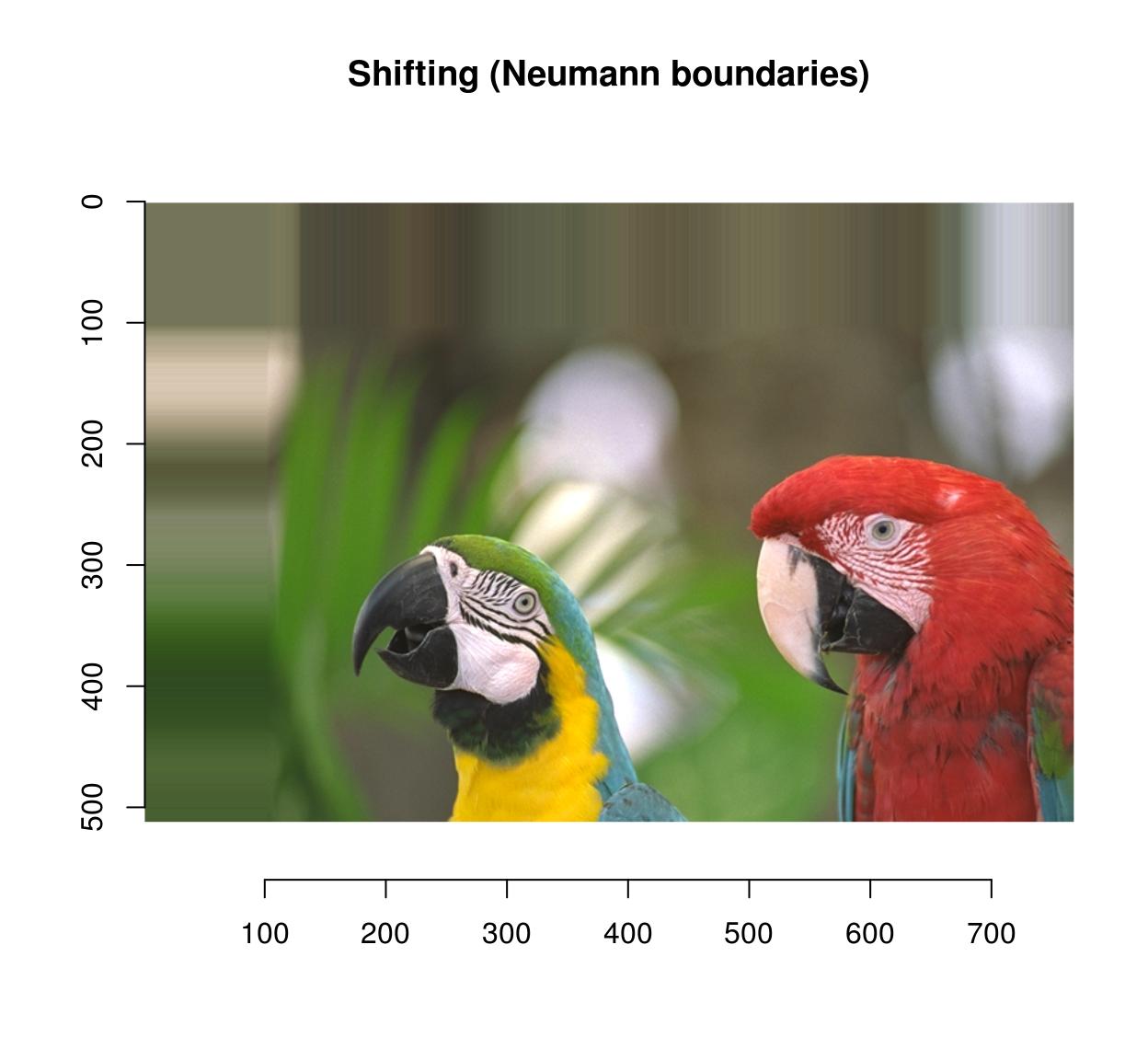

            imshift(parrots,100,100,boundary=2) %>% plot(main="Shifting (circular)")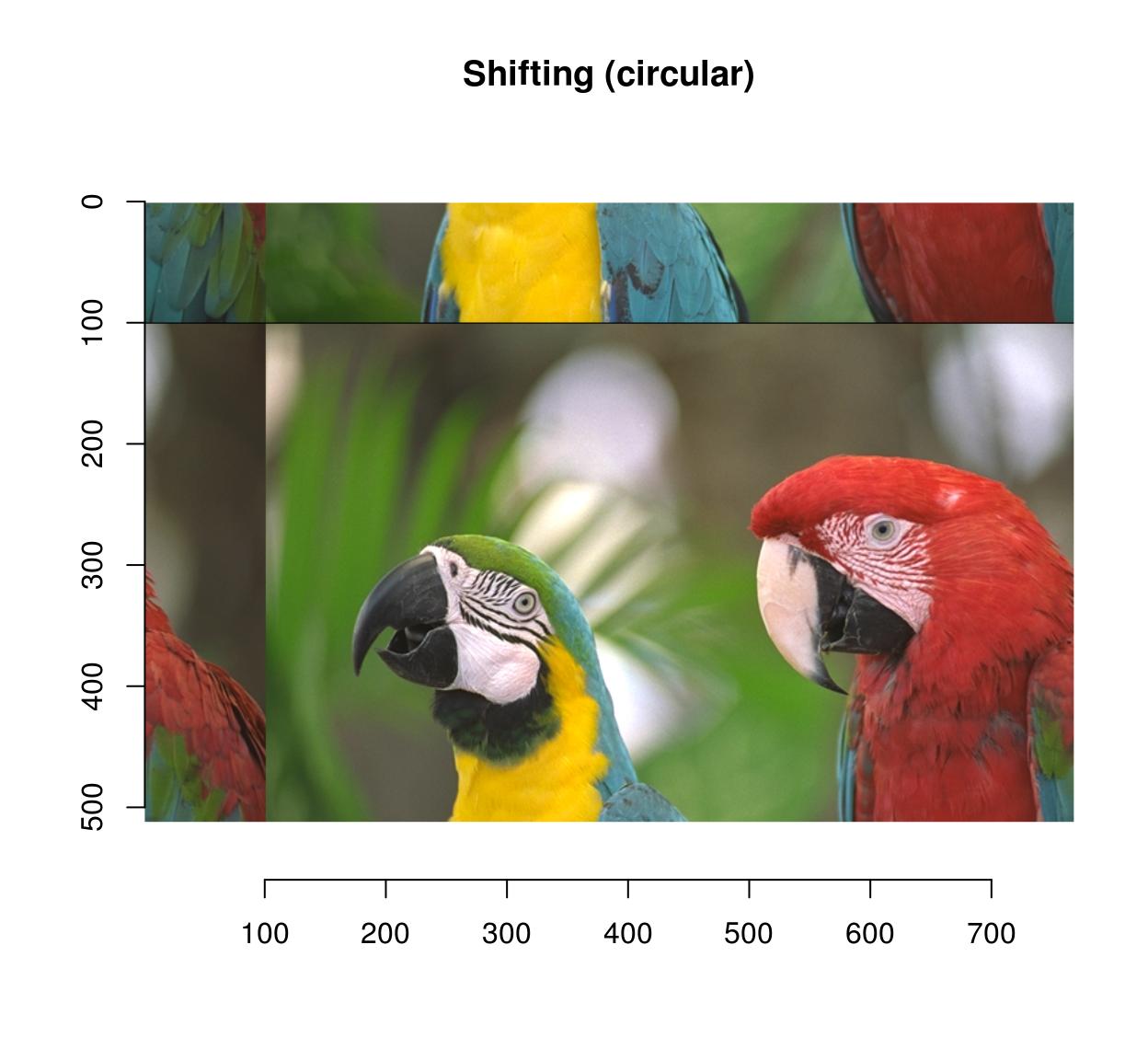

Yous can pad an image using "pad":

            pad(parrots,axes="y",140) %>% plot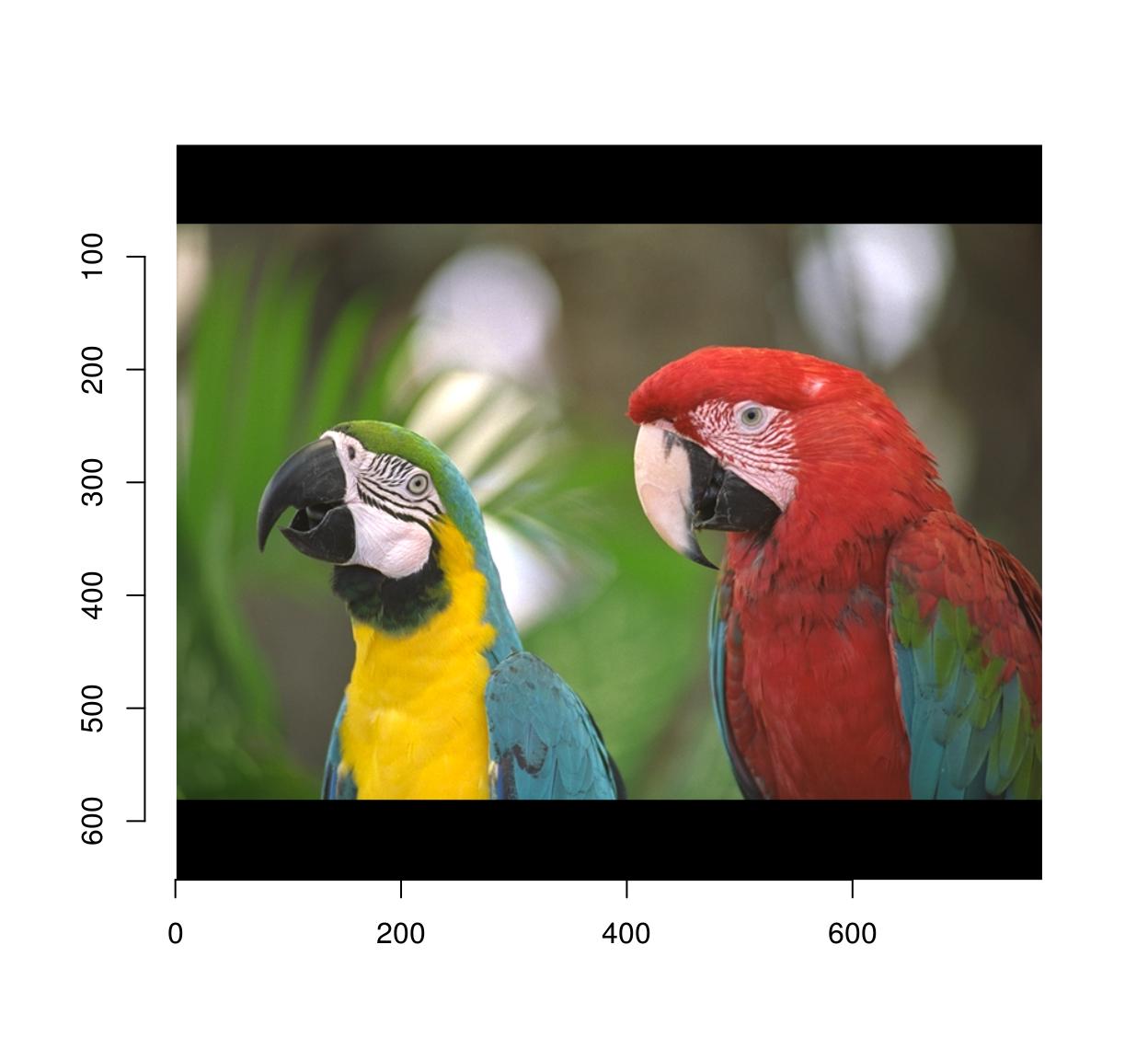

            pad(parrots,axes="y",140,pos=-i) %>% plot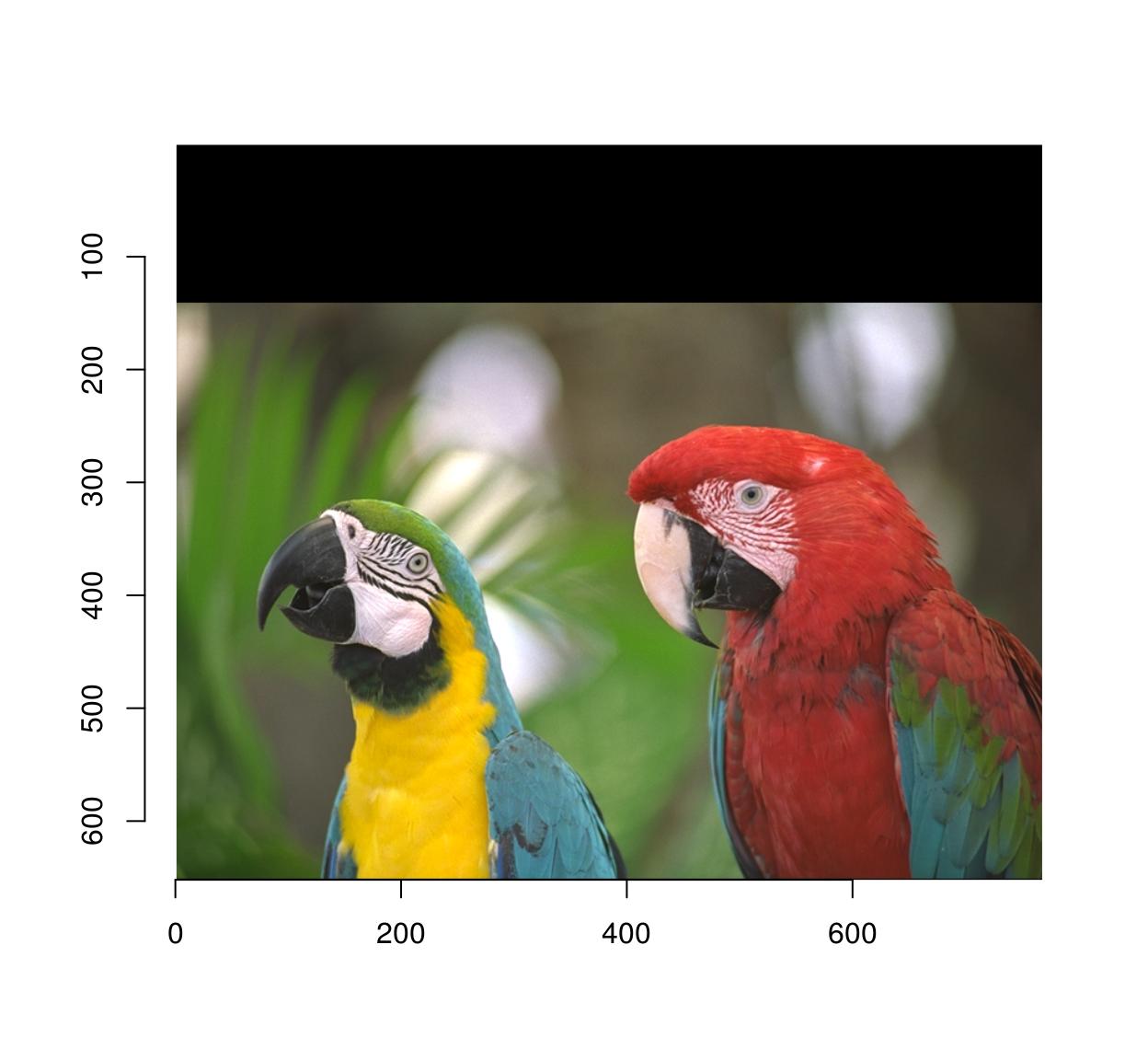

autocrop volition remove whatsoever extra padding:

            #The argument to autocrop is the colour of the groundwork information technology needs to remove pad(parrots,axes="y",140,pos=-one) %>% autocrop(c(0,0,0)) %>% plot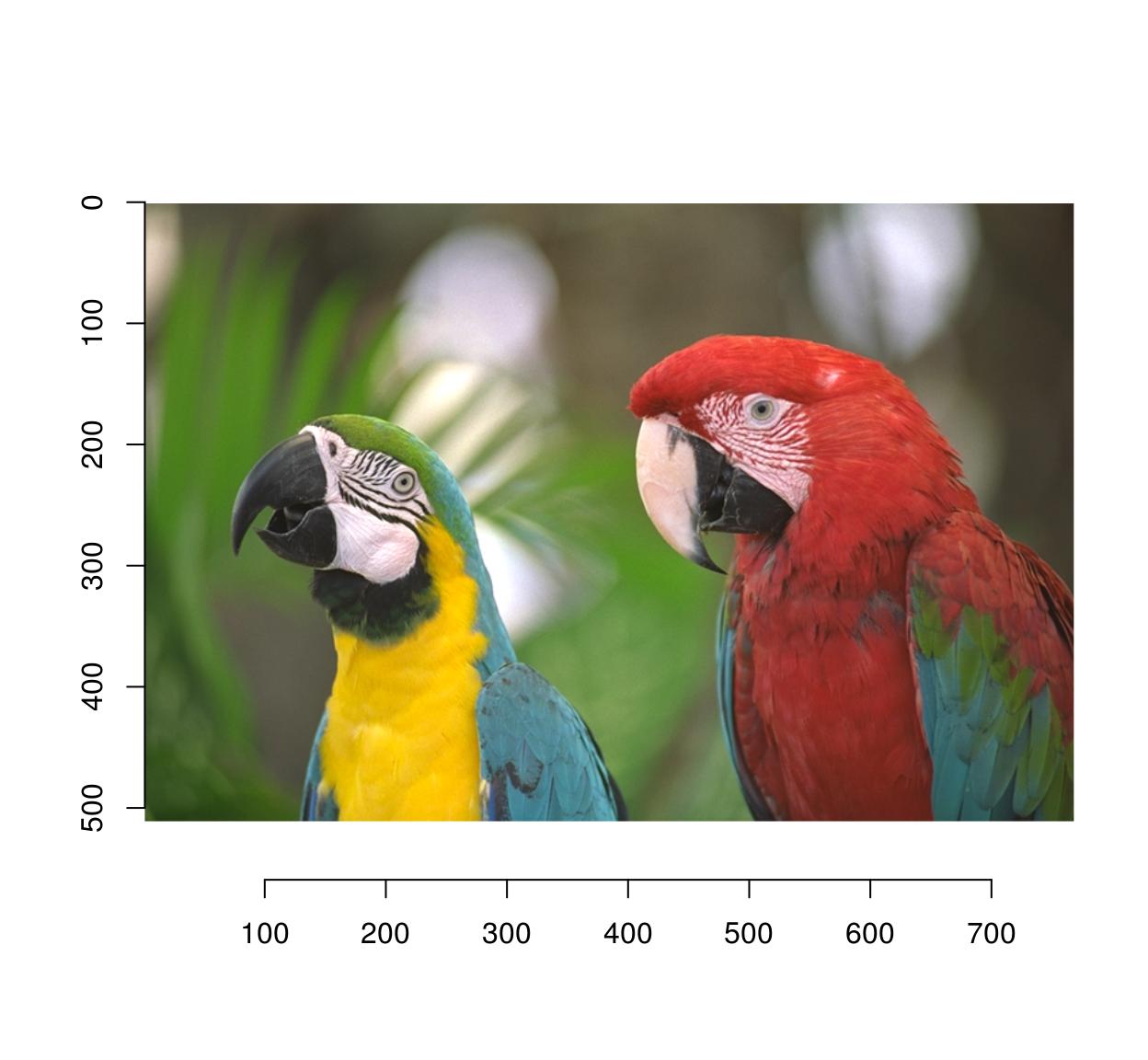

Warping

Warping maps the pixels of the input paradigm to a dissimilar location in the output. Scaling is a special case of warping, so is shifting. Warping relies on a map: \(1000(x,y) = (x',y')\)

that describes where to send pixel (10,y). Shifting the image corresponds to adding a constant to the coordinates: \(M(x,y) = (x+\delta_x,y+\delta_y)\)

In imager:

            map.shift <- function(x,y) list(x=x+10,y=y+30) imwarp(parrots,map=map.shift) %>% plot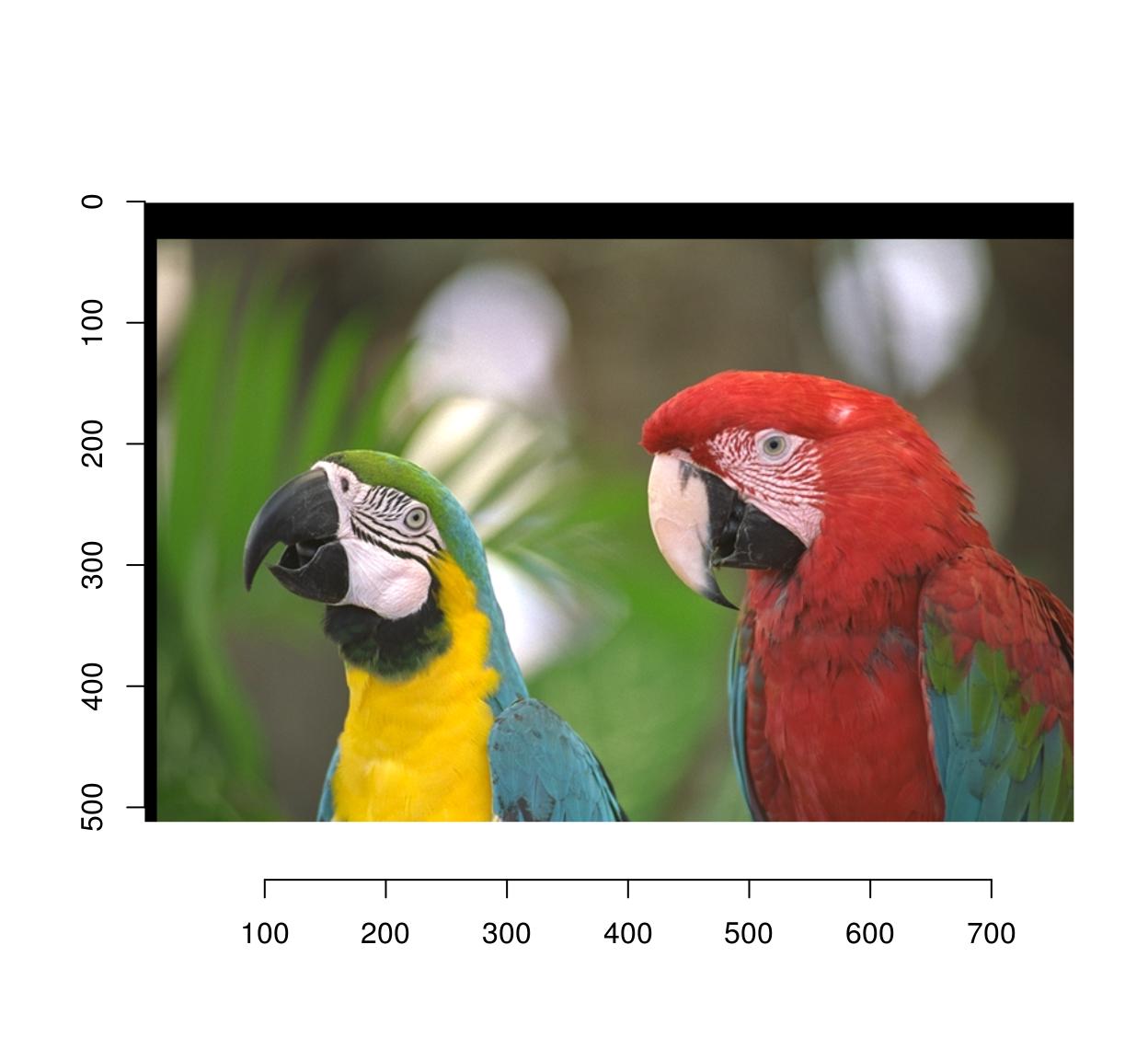

The map function should accept (x,y) every bit arguments and output a named list with values (x,y).

The warping algorithm has two modes, "forward" and "astern". In forward way you go through all \((x,y)\) pixels in the source, and paint the respective location \(One thousand(x,y)\) in the target image. This may result in unpainted pixels, every bit in the following example:

            map.calibration <- function(x,y) listing(ten=1.v*x,y=1.5*y) imwarp(parrots,map=map.scale) %>% plot(main="Forward mode")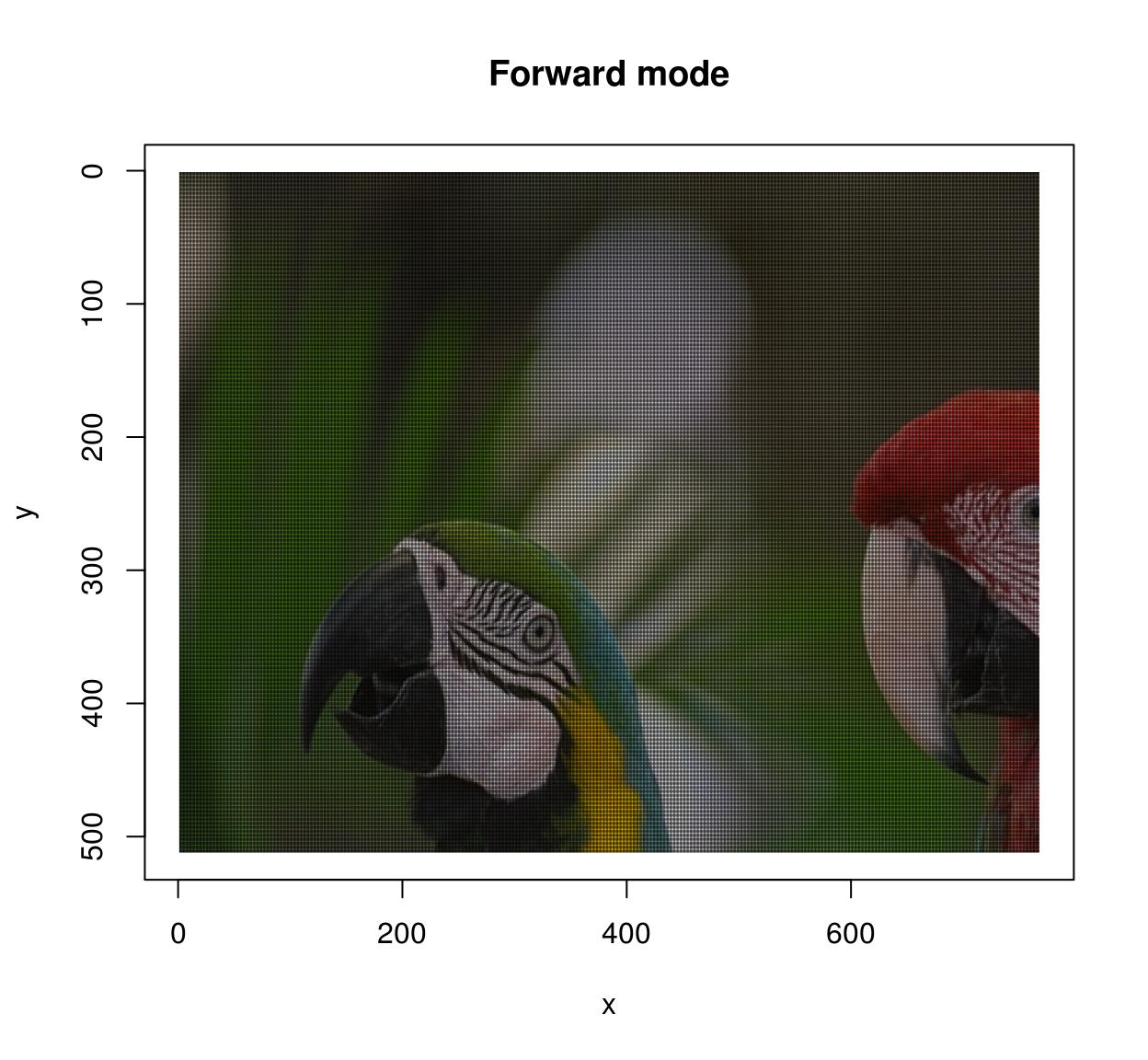

In backward mode you get through all pixels \((x',y')\) in the target image, and wait up their antecedent \(M^{-one}(x',y')\) in the source image. Backward mode has no missing pixel problems, merely at present you need to ascertain the inverse map and set the "direction" statement to "astern".

            map.scale.bw <- function(ten,y) list(10=x/i.5,y=y/one.5) imwarp(parrots,map=map.calibration.bw,direction="backward") %>% plot(main="Backward way")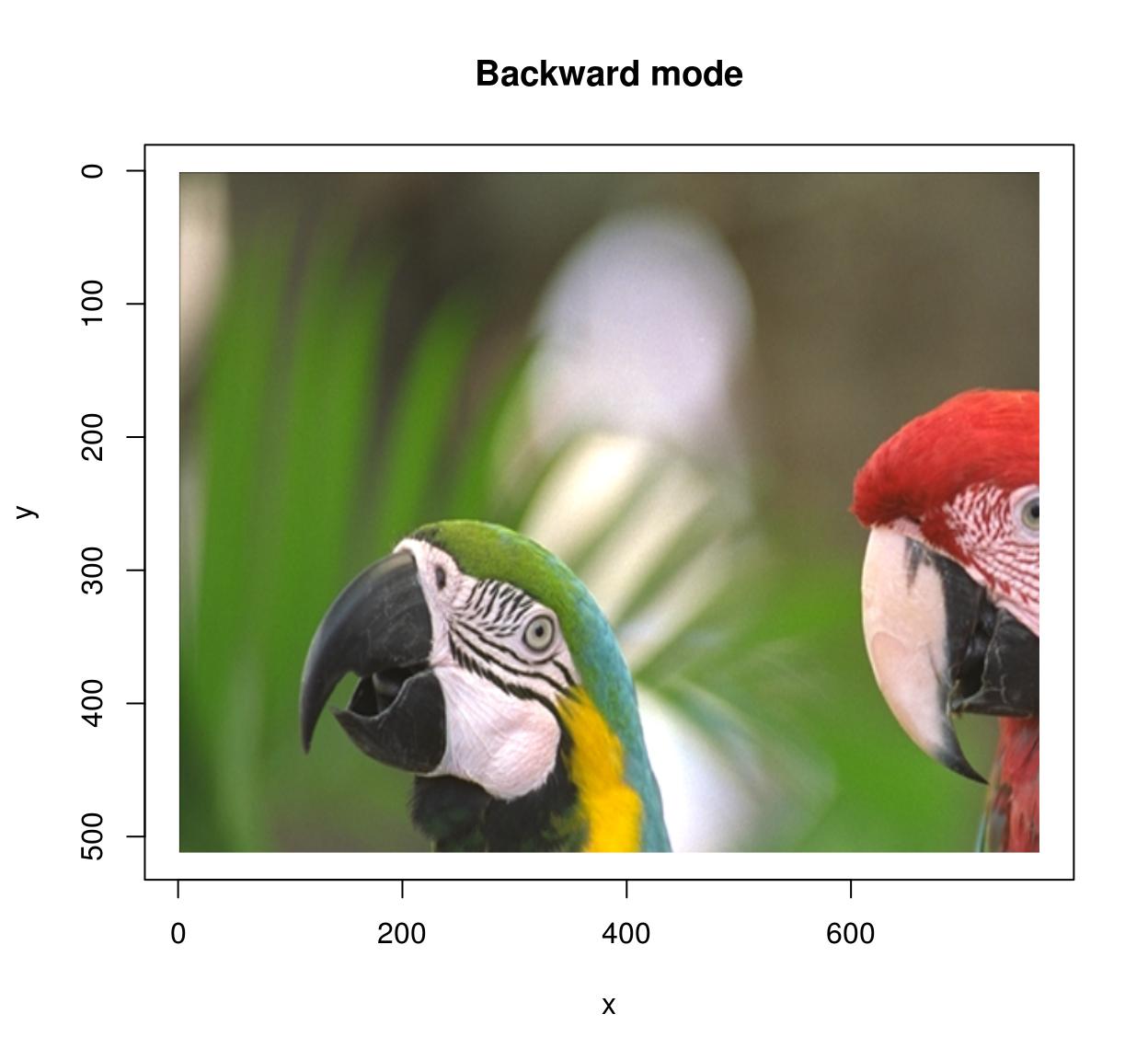

Of course shifting and scaling things is boring and the whole point of warping is to do things similar that:

            map <- role(x,y) listing(x=exp(y/600)*x,y=y*exp(-sin(x/40))) imwarp(parrots,map=map,direction="frontwards") %>% plot()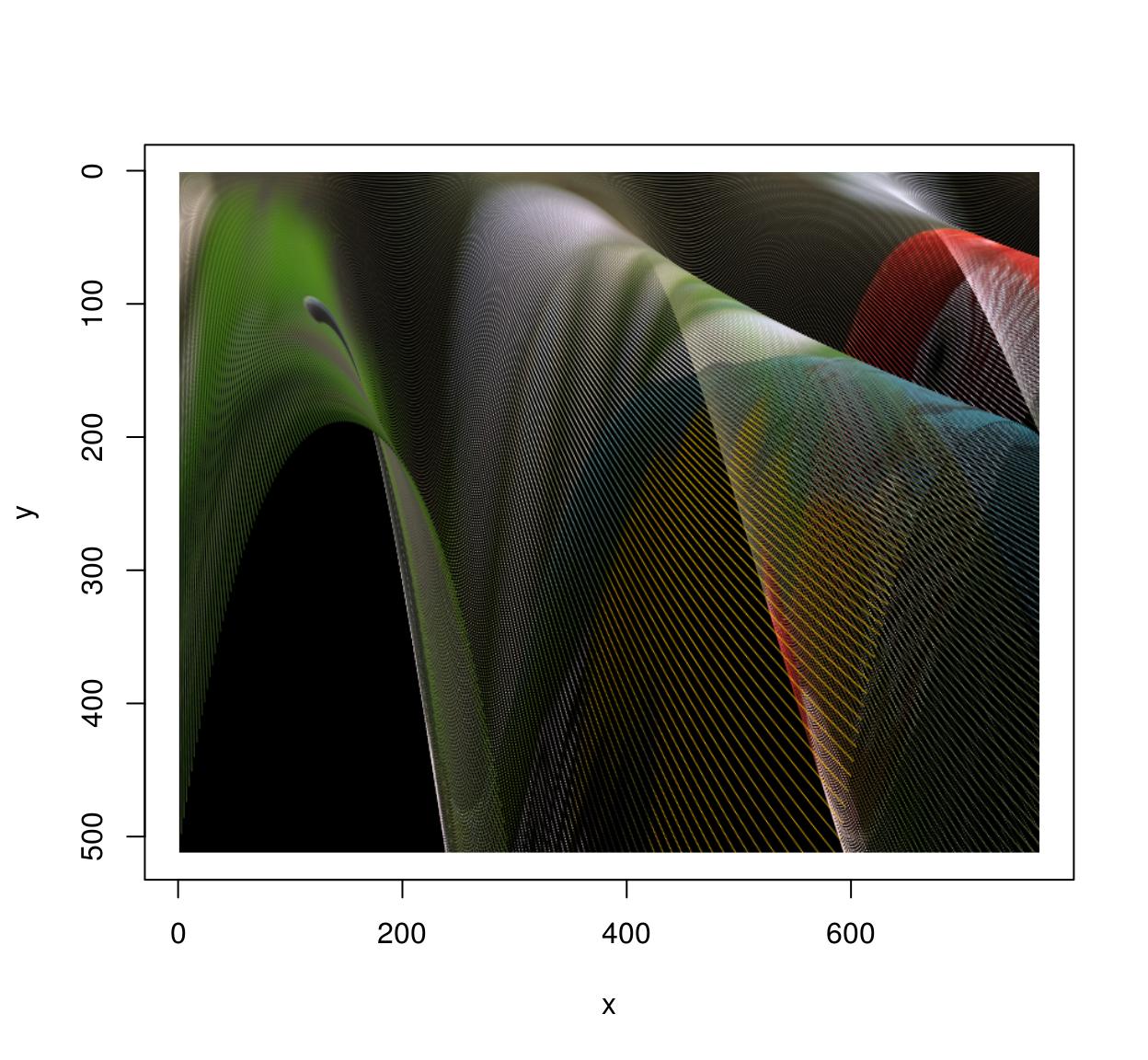

Run across ?imwarp for more. Note that 3D warping is possible equally well.

Lagged operators

To compute the difference between successive images in a video, you lot can use the shift operator:

            #Compute divergence between two successive frames (at lag 1) (imshift(tennis,delta_z=1)-lawn tennis) %>% plot(frame=2,chief="Departure betw. frames 2 and ane")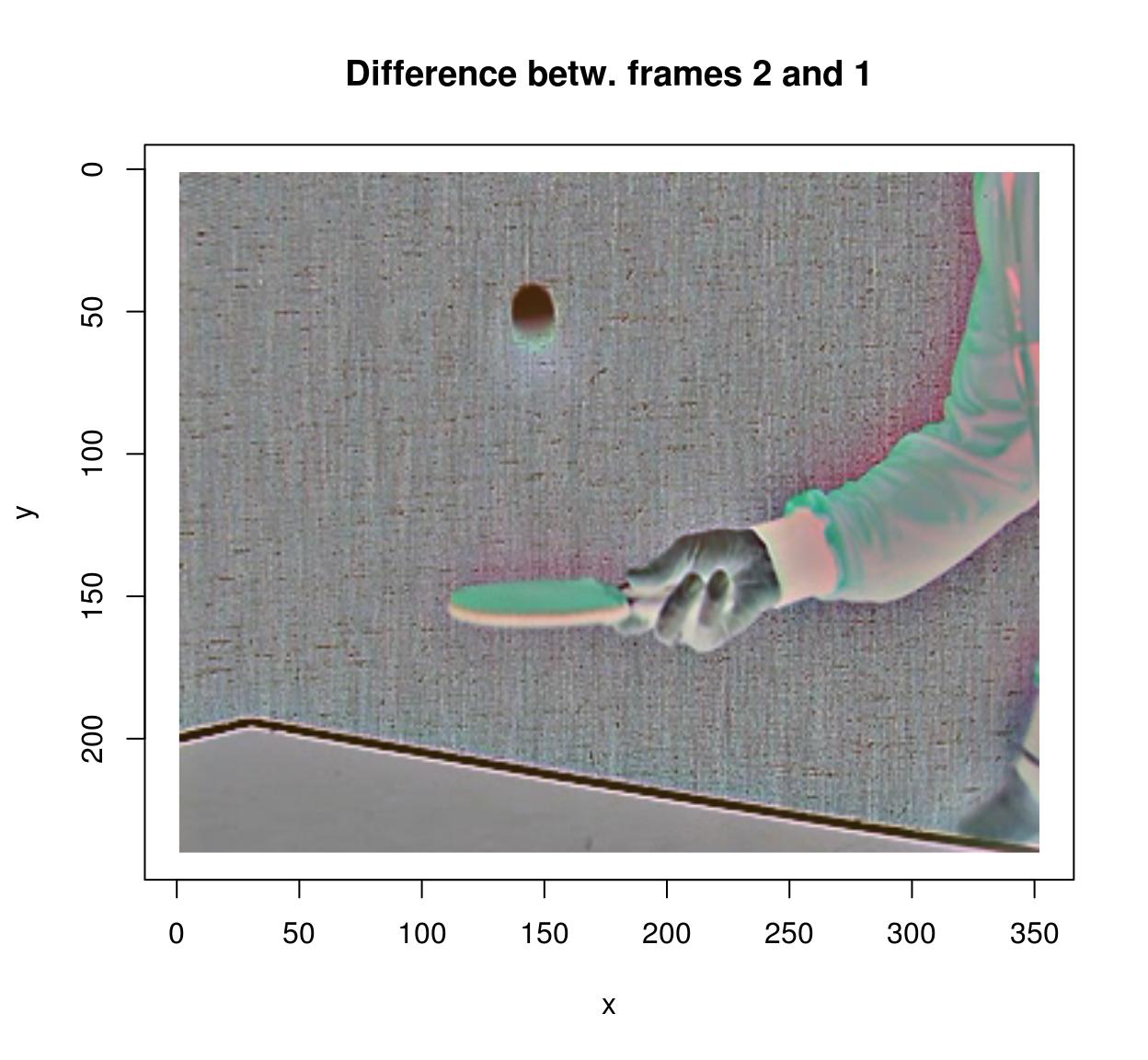

            #Compute departure between frames (at lag 3) (imshift(lawn tennis,delta_z=3)-tennis) %>% plot(frame=iv,main="Difference between frames 3 and i")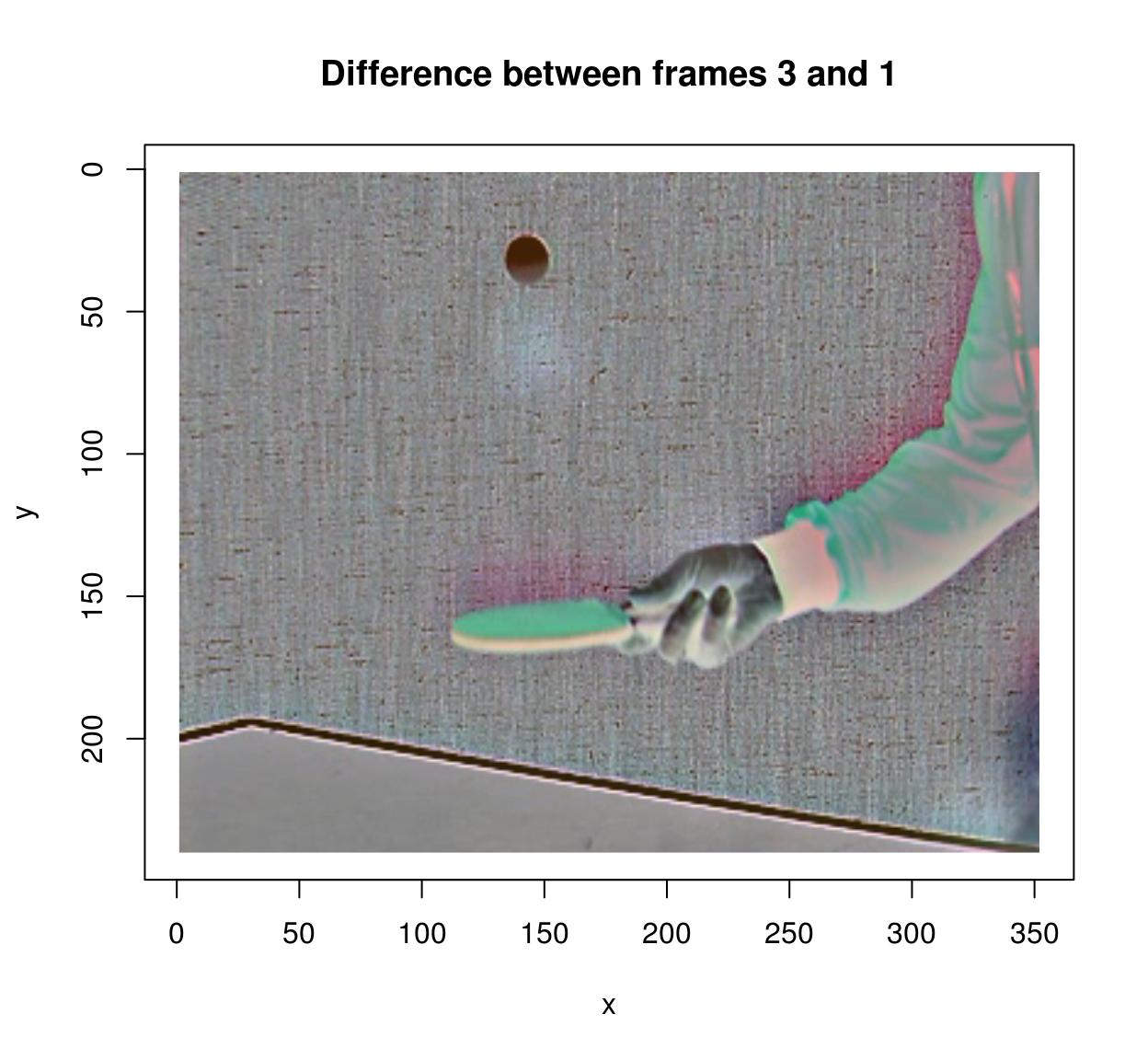

            #note that shift uses interpolation. that makes it relatively slow, but one advantage is that information technology allows non-integer lags: #shift(lawn tennis,delta_z=3.5)-tennis #is valid

Filtering

imager has the usual correlate and convolve operations:

            flt <- as.cimg(matrix(i,4,iv)) #4x4 box filter grayscale(parrots) %>% correlate(flt) %>% plot(master="Filtering with box filter")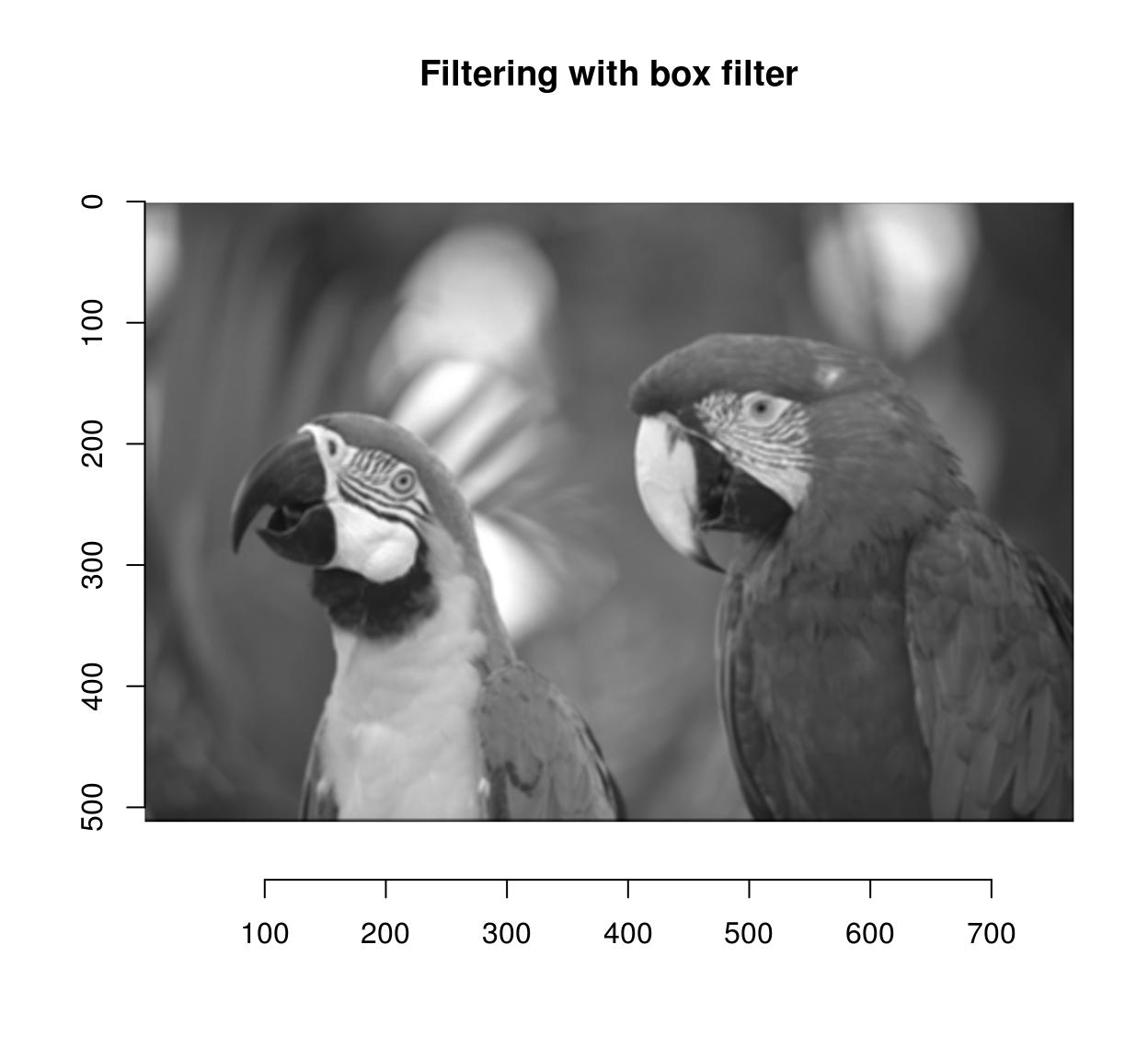

            #Here the filter is symmetrical so convolution and correlation should be the same. Bank check: a <- grayscale(parrots) %>% correlate(flt) b <- grayscale(parrots) %>% imager::convolve(flt) all.equal(a,b)

            [1] "Hateful relative departure: 0.02401757"

CImg includes fast implementations of Gaussian (and derivative-of-Gaussian) filters. They are available via the "deriche" and "vanvliet" functions.

            im <- grayscale(parrots) layout(t(1:ii)) deriche(im,sigma=iv,order=2,axis="y") %>% plot(chief="2d deriv of Gaussian along y") vanvliet(im,sigma=4,society=2,axis="y") %>% plot(principal="2nd deriv of Gaussian along y")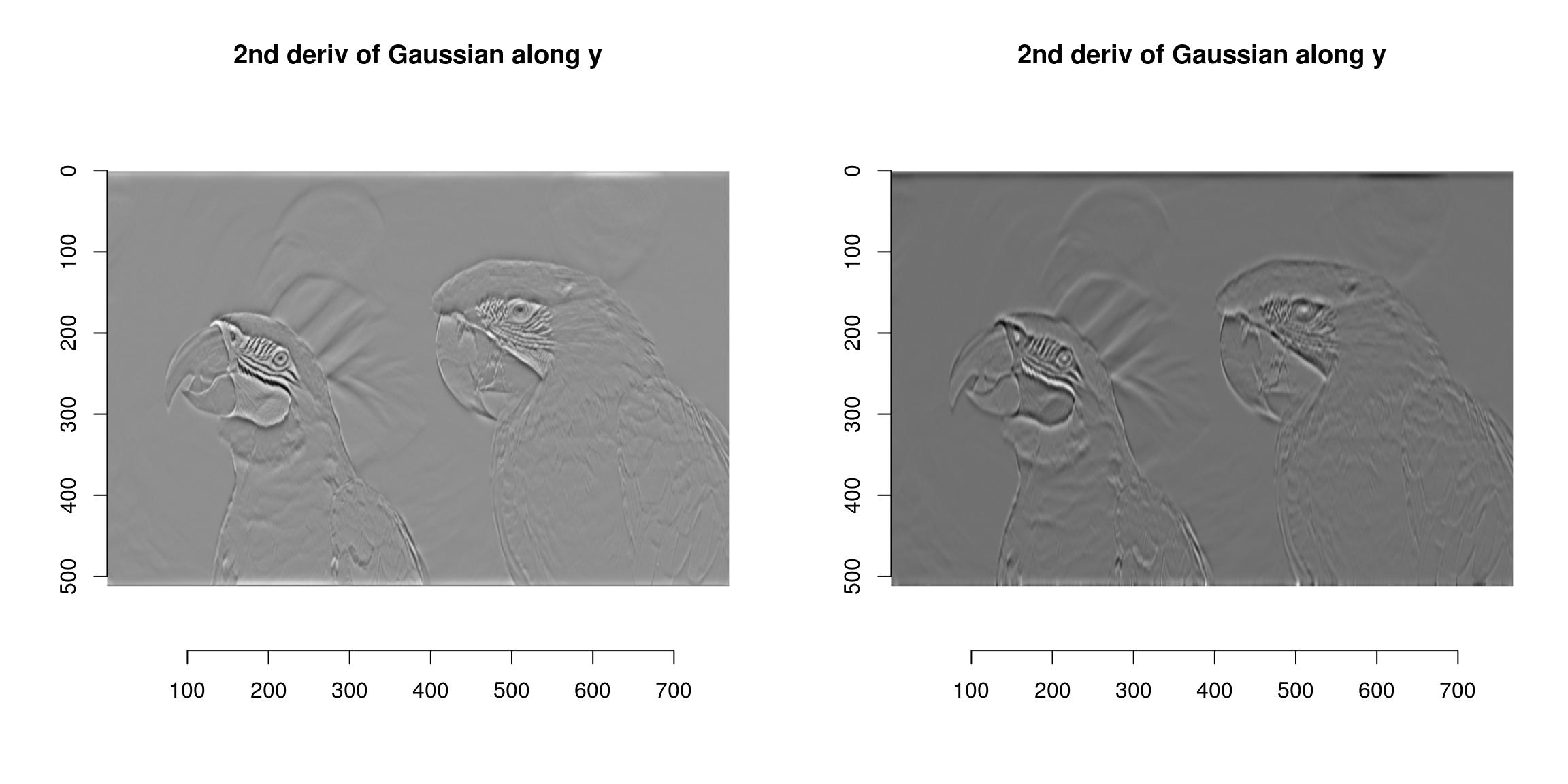

The Vanvliet-Young filter is typically a better approximation. We can plant this by looking at the impulse response (which should be Gaussian). Here'due south the one-dimensional case:

            n <- 1e3 fifteen <- seq(0,one,l=n) #1D Grid imp <- imdirac(c(n,ane,i,i),n/ii,ane) #1D betoken: Impulse at ten = n/2 sig <- 80 #impulse response of the Deriche filter imp.dr <- deriche(imp,sigma=sig) %>% as.vector #impulse response of the Vanvliet-Young filter imp.vv <- vanvliet(imp,sigma=sig) %>% equally.vector  imp.true <- dnorm(xv,sd=sig/n,m=.five) #True impulse response plot(fifteen,imp.true/max(imp.truthful),blazon="l",lwd=2,xlab="x",ylab="Impulse response") lines(xv,imp.vv/max(imp.vv),col="bluish",lwd=two) lines(xv,imp.dr/max(imp.dr),col="red",lwd=2)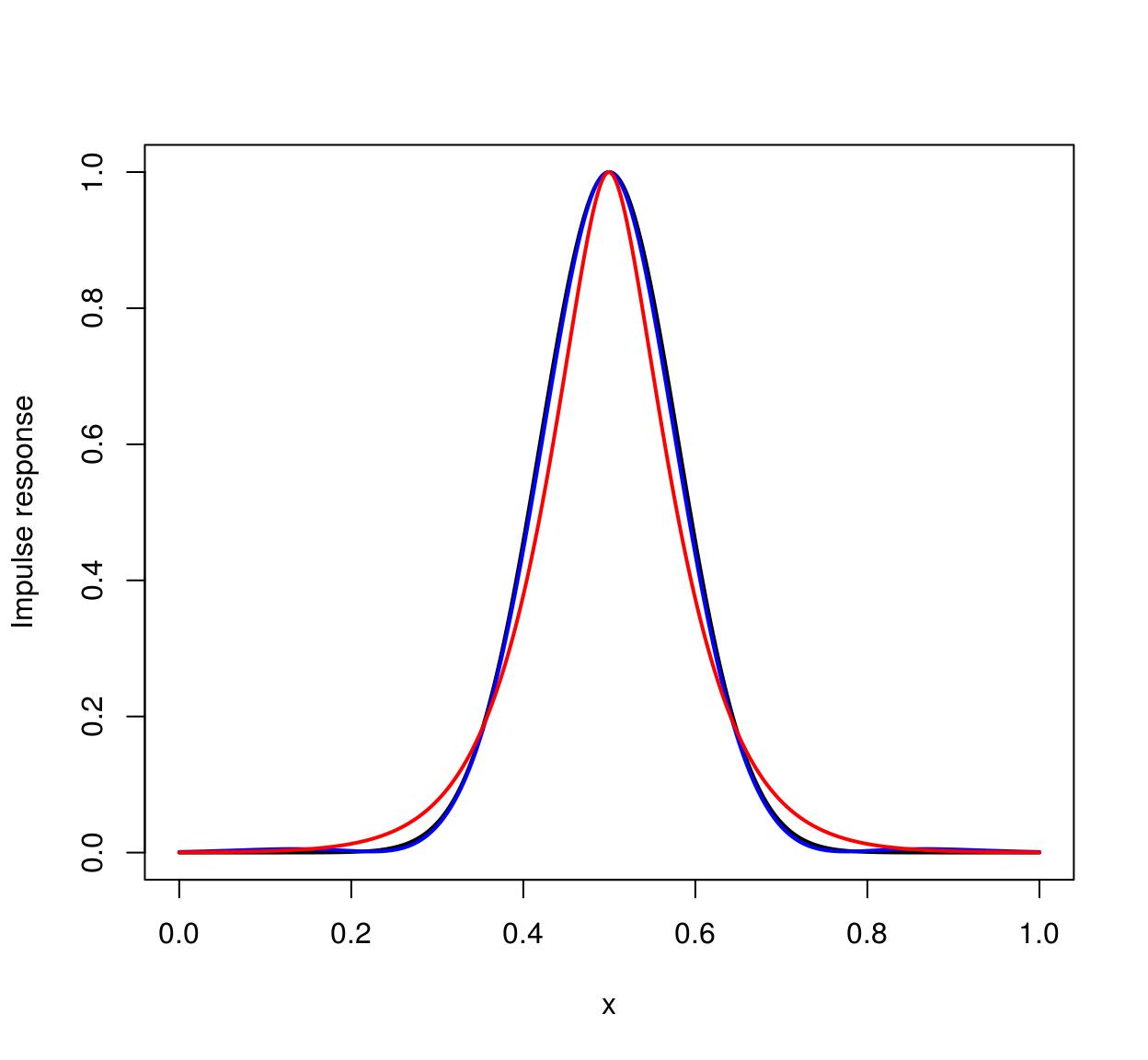

The ideal filter is in black, the Vanvliet-Young filter in blue, the Deriche filter in red. Vanvliet-Immature is clearly more accurate, but slightly slower:

            im <- imfill(3e3,3e3) system.time(deriche(im,3))

                          user  arrangement elapsed    0.096   0.012   0.042

            system.time(vanvliet(im,3))

                          user  system elapsed    0.168   0.004   0.047

In both cases computation fourth dimension is independent of filter bandwidth, which is a very nice feature (the filters are IIR).

FFTs and the periodic/shine decomposition

FFTs can be computed via the FFT role:

            im <- as.cimg(function(x,y) sin(x/5)+cos(x/4)*sin(y/2),128,128) ff <- FFT(im) plot(ff$existent,main="Existent part of the transform")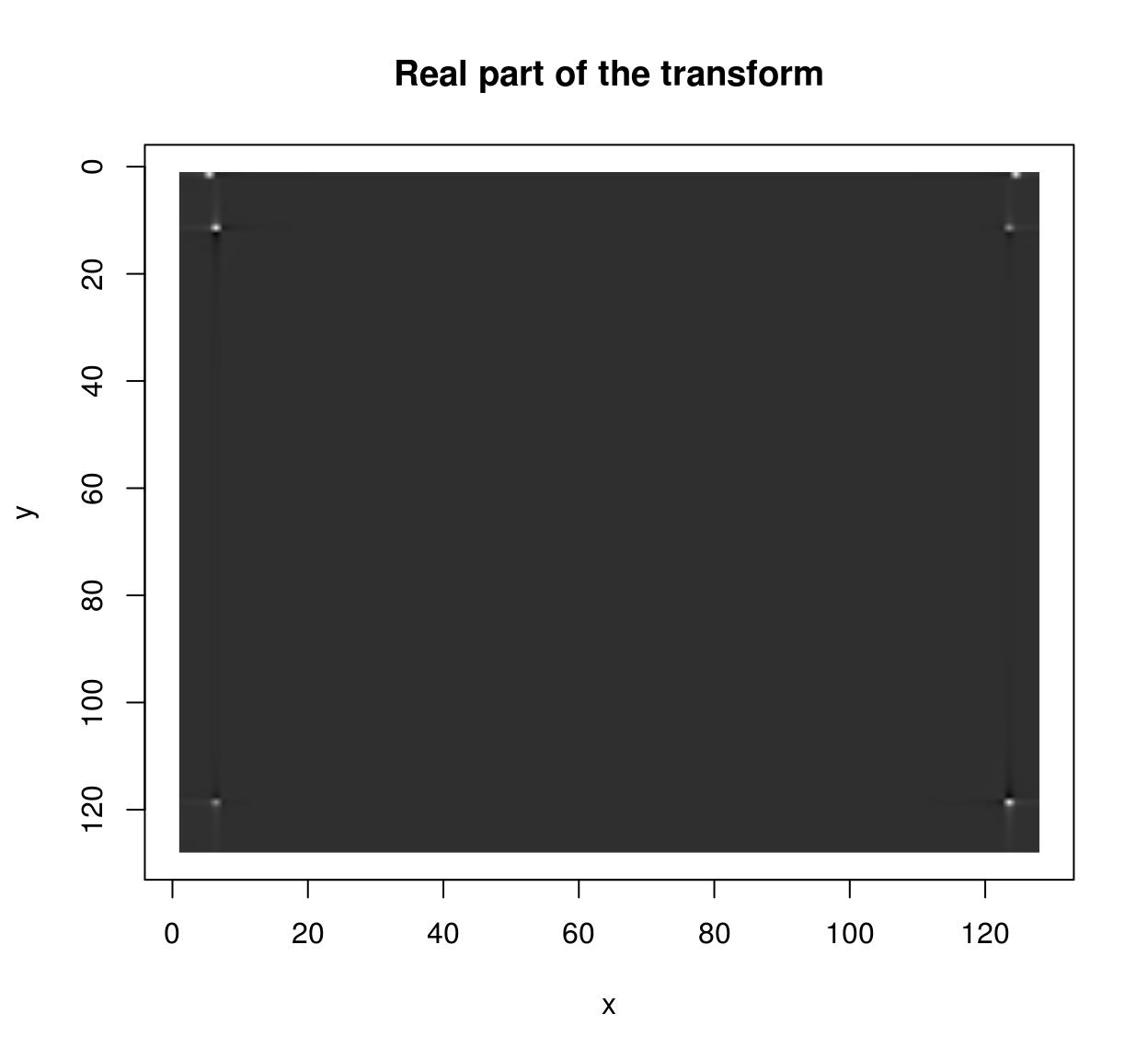

            plot(ff$imag,main="Imaginary part of the transform")

            sqrt(ff$real^2+ff$imag^2) %>% plot(primary="Ability spectrum")

If yous desire to use CImg's FFT on images of arbitrary size you lot should enable FFTW3 back up. Install FFTW3 on your system, then run install_github("dahtah/imager",ref="fftw"). As a workaround you can also use R'southward native fft:

            rff <- as.matrix(im) %>% fft Re(rff) %>% as.cimg %>% plot(chief="Real part of the transform (R's native code)")

Of import: both FFT and fft volition effort to perform a multi-dimensional FFT of the input, with dimensionality divers by the dimensionality of the assortment. If you want to compute a 2nd FFT for every frame of a video, apply a split (imsplit or ilply).

The FFT works all-time for periodic signals. One manner of making signals periodic is via zero-padding (use the pad function), another is to use the periodic-shine decomposition of Moisan (2011):

            layout(t(1:ii)) periodic.part(parrots) %>% plot(main="Periodic role of parrots") (parrots- periodic.function(parrots)) %>% plot(chief="Smooth residual of parrots")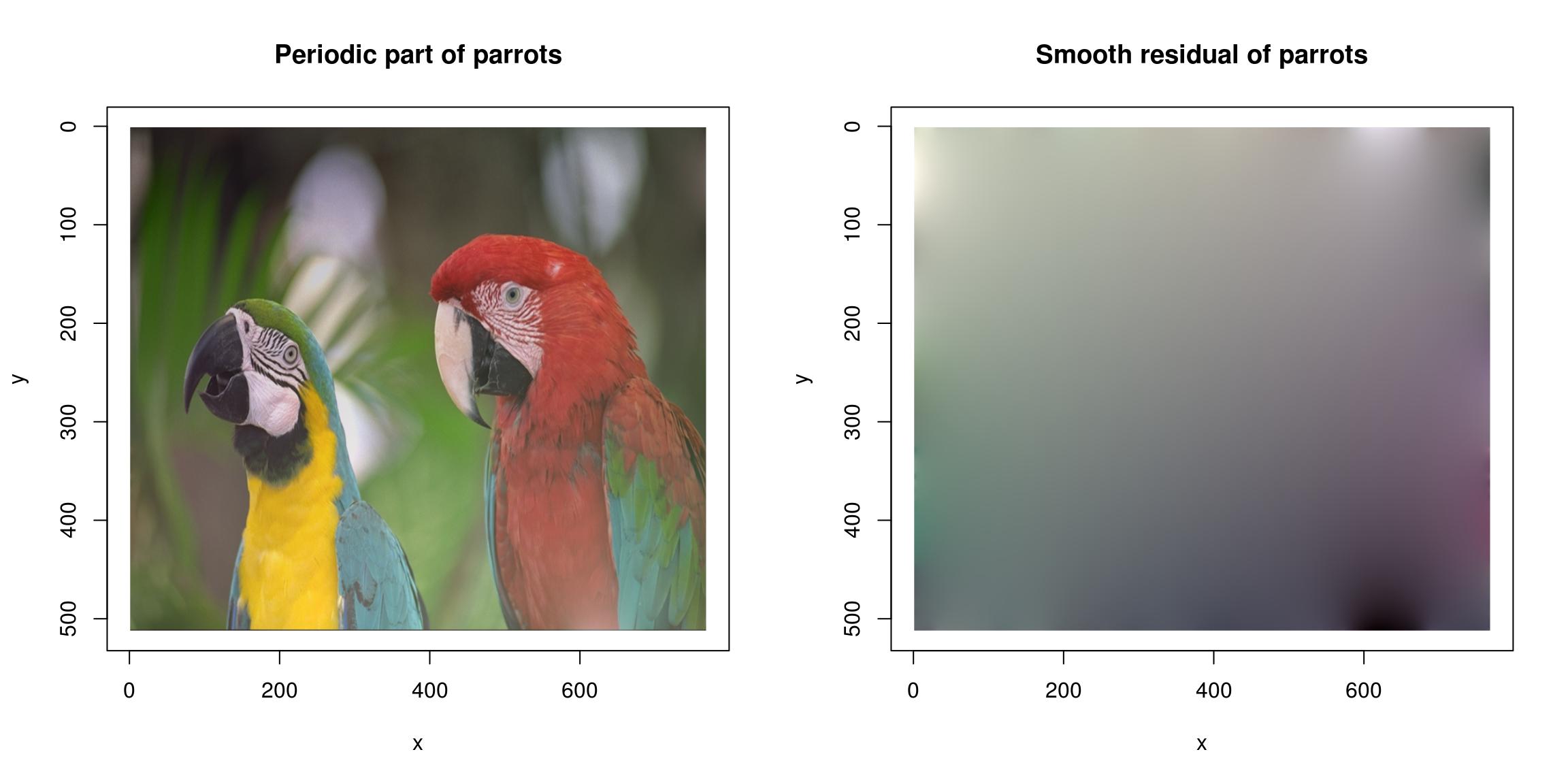

Meet ?periodic.shine for details.

swishergramptude.blogspot.com

Source: https://dahtah.github.io/imager/imager.html